Question

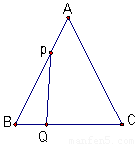
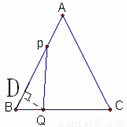
已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t(s)，解答下列各问题：

（1）求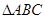的面积；

（2）当t为何值是，△PBQ是直角三角形？

（3）设四边形APQC的面积为y(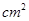)，求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是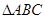面积的三分之二？如果存在，求出t的值；不存在请说明理由.

 

Answer 1

【答案】

（1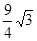）；（2）t=2或t=1；（3）不存在

【解析】

试题分析：（1）根据等边三角形的性质及三角形的面积公式求解即可；

（2）由题意此时P点和Q点移动距离为tcm，所以AP=BQ=tcm，BP=AB-AP=3-tcm，则在△PBQ中，∠B=60°，BP=3-t，BQ=t，分①当PQ⊥BC时，则∠BPQ=30°，②当PQ⊥BA时，则∠BQP=30°，两种情况，结合含30°角的直角三角形的性质求解即可；

（3）作QD⊥AB于D，则，根据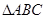的面积可表示出△BQD的面积，从而可得y与t的函数关系式，即可得到关于t的方程，由方程的根的判别式△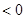即可作出判断.

（1）；

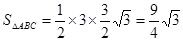（2）此时P点和Q点移动距离为tcm，所以AP=BQ=tcm，BP="AB-AP=3-tcm"

在△PBQ中，∠B=60°，BP=3-t，BQ=t

①当PQ⊥BC时，则∠BPQ=30°

∴BP=2BQ，即3-t=2t

∴t=1；

②当PQ⊥BA时，则∠BQP=30°

∴BQ=2BP，即2（3-t）=t

∴t=2                 

综上所述，t=2或t=1；

（3）作QD⊥AB于D，则 

∵

∴  

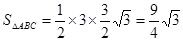
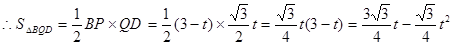
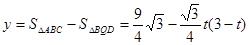
当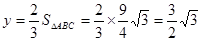

∴              

化简得：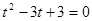

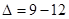
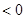
∴不存在这样的t.

考点：动点的综合题

点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．