
【题目】如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.
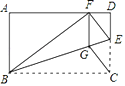
(1)求证:四边形CEFG是菱形;
(2)若AB=6,AD=10,求四边形CEFG的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意和翻折的性质,可以得到△BCE≌△BFE,再根据全等三角形的性质和菱形的判定方法即可证明结论成立;
(2)根据题意和勾股定理,可以求得AF的长,进而求得EF和DF的值,从而可以得到四边形CEFG的面积.
(1)证明:由题意可得,△BCE≌△BFE,
∴∠BEC=∠BEF,FE=CE,
∵FG∥CE,
∴∠FGE=∠CEB,
∴∠FGE=∠FEG,
∴FG=FE,
∴FG=EC,
∴四边形CEFG是平行四边形,
又∵CE=FE,
∴四边形CEFG是菱形;
(2)∵矩形ABCD中,AB=6,AD=10,BC=BF,
∴∠BAF=90°,AD=BC=BF=10,
∴AF=8,
∴DF=2,
设EF=x,则CE=x,DE=6﹣x,
∵∠FDE=90°,
∴22+(6﹣x)2=x2,
解得,x=![]() ,
,
∴CE=![]() ,
,
∴四边形CEFG的面积是:CEDF=![]() ×2=
×2=![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】尺规作图要求: I、过直线外一点作这条直线的垂线: II、 作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
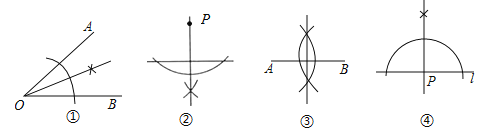
则正确的配对是( )
A.①-IV,②-II,③-I,④-IIIB.①-IV, ②-I,③-II,④-I
C.①-II,②-IV,③-1II,④-ID.①-IV,②-I,③-II,④-III
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点
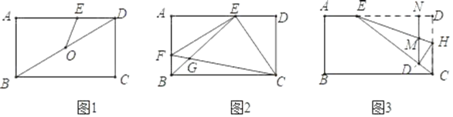
(1)如图 1,连接 BD,O 是对角线 BD 的中点,连接 OE.当 OE=DE 时,求 AE 的长;
(2)如图 2,连接 BE,EC,过点 E 作 EF⊥EC 交 AB 于点 F,连接 CF,与 BE 交于点 G.当BE 平分∠ABC 时,求 BG 的长;
(3)如图 3,连接 EC,点 H 在 CD 上,将矩形 ABCD 沿直线 EH 折叠,折叠后点 D 落在 EC上的点 D′处,过点 D′作 D′N⊥AD 于点 N,与 EH 交于点 M,且 AE=1.![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
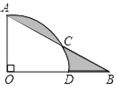
【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
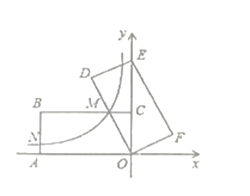
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
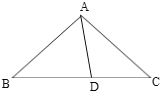
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》内容主要讲数学的用途,浅显易懂,其中有许多有趣的数学题,如“河边洗碗”.原文:今有妇人河上荡桮.津吏问曰:“桮何以多?“妇人曰:“家有客.”津吏曰:“客几何?”妇人日:“二人共饭,三人共羹,四人共肉,凡用桮六十五.不知客几何?“译文:有一名妇女在河边洗刷一大摞碗.一个津吏问她:“怎么刷这么多碗呢?“她回答:“家里来客人了.“津吏又问:“家里来了多少客人?”妇女答道:“2个人给一碗饭,3个人给一碗汤,4个人给一碗肉,一共要用65只碗,来了多少客人?”答:共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
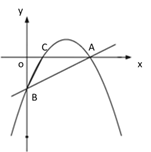
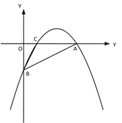
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
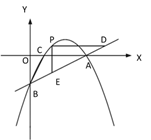
① ② ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com