

���� ��1������������Խ���⣻
��2��������ѧ���ɷ���д��ǰ�����ܽ���ɣ��Ӷ����Խ���⣻
��3��������ѧ���ɷ���д��ǰ�����ܽ���ɣ��Ӷ����Խ���⣮
��� �⣺��1��������ɵã�
��a+b��7��չ��ʽ���а�����е������ϵ��Ϊ��6+15=21��
�ʴ�Ϊ���ˣ�21��
��2���ߵ�n=1ʱ������ʽ��a+b��1չ��ʽ�ĸ���ϵ��֮��Ϊ��1+1=2=21��
��n=2ʱ������ʽ��a+b��2չ��ʽ�ĸ���ϵ��֮��Ϊ��1+2+1=4=22��
��n=3ʱ������ʽ��a+b��3չ��ʽ�ĸ���ϵ��֮��Ϊ��1+3+3+1=8=23��
��n=4ʱ������ʽ��a+b��4չ��ʽ�ĸ���ϵ��֮��Ϊ��1+4+6+4+1=16=24��
��
�����ʽ��a+b��9չ��ʽ�ĸ���ϵ��֮��=29��
��3���ߵ�n=1ʱ������ʽ��a+b��1չ��ʽ�ĸ���ϵ��֮��Ϊ��1+1=2=21��
��n=2ʱ������ʽ��a+b��2չ��ʽ�ĸ���ϵ��֮��Ϊ��1+2+1=4=22��
��n=3ʱ������ʽ��a+b��3չ��ʽ�ĸ���ϵ��֮��Ϊ��1+3+3+1=8=23��
��n=4ʱ������ʽ��a+b��4չ��ʽ�ĸ���ϵ��֮��Ϊ��1+4+6+4+1=16=24��
��
�����ʽ��a+b��nչ��ʽ�ĸ���ϵ��֮�ͣ�S=2n��
�ʴ�Ϊ��2n��
���� ���⿼����ʽ�Ļ�����ֵ�����ֵı仯������Ĺؼ�����ȷ���⣬������ѧ���ɷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
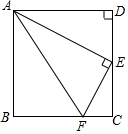 ����ABCD��CD=6��E��CD�е㣬F��BC����һ�㣬��Rt��ABF��AF���۵�Bǡ������E������AF�ij���
����ABCD��CD=6��E��CD�е㣬F��BC����һ�㣬��Rt��ABF��AF���۵�Bǡ������E������AF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
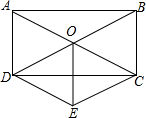 ��ͼ������ABCD�������Խ��߽��ڵ�O��DE��AC��CE��DB��DE��CE���ڵ�E����֤��OE��CD���ഹֱƽ�֣�
��ͼ������ABCD�������Խ��߽��ڵ�O��DE��AC��CE��DB��DE��CE���ڵ�E����֤��OE��CD���ഹֱƽ�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
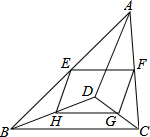 ��ͼ��D�ǡ�ABC��һ�㣬E��F��G��H�ֱ���AB��AC��CD��BD���е㣬��֤���ı���EFGH��ƽ���ı��Σ�
��ͼ��D�ǡ�ABC��һ�㣬E��F��G��H�ֱ���AB��AC��CD��BD���е㣬��֤���ı���EFGH��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
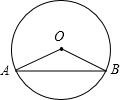 ��1����ͼ����AB�ѡ�O�ֳ�2��7����AOB=80�㣻
��1����ͼ����AB�ѡ�O�ֳ�2��7����AOB=80�㣻�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com