Question

3．如图，在△ABC中，∠A=2∠B，且∠A、∠B、∠C的对边分别为a、b、c．
（1）若∠B=36°，b=1，则c=$\frac{\sqrt{5}+1}{2}$；
（2）如图1，若a=6，b=4，则c的值；
（3）如图2，若∠A=2∠B=4∠C．若c=3，求$\frac{a+b}{ab}$的值．

Answer 1

分析 （1）如图1中，作∠ACB的平分线CE交AB于E．设AE=x，由△ACE∽△ABC，得$\frac{AC}{AB}$=$\frac{AE}{AC}$，列出方程即可解决问题．
（2）如图2中，过点A作∠BAC的平分线交BC于D，作DE⊥AB于E，DF⊥AC于F，设AE=x，由△CAD∽△CBA，得$\frac{CD}{AC}$=$\frac{AC}{BC}$，列出方程求出x，再由$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$=$\frac{\frac{1}{2}•AB•DE}{\frac{1}{2}•AC•DF}$=$\frac{AB}{AC}$，即可求出出AB，解决问题．
（3）如图3中，过点A作AD平分∠BAC交BC于D，过点A作∠DAC的平分线交CD于E，首先证明DA=DB，AB=AE=EC，设DB=DA=x，则DE=a-c-x，由△ADE∽△CAB，得到$\frac{DE}{AB}$=$\frac{AD}{AC}$，即$\frac{a-c-x}{c}$=$\frac{x}{b}$     ①，由$\frac{AD}{AC}$=$\frac{DE}{CE}$，得到$\frac{x}{c}$=$\frac{a-x}{b}$         ②，由①②消去x，进行变形即可解决问题．

解答 解：（1）如图1中，作∠ACB的平分线CE交AB于E．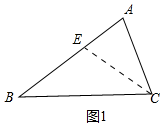

∵∠A=2∠B，∠B=36°，
∴∠A=72°，∠ACB=180°-∠B-∠A=72°，
∴∠ACE=∠BCE=36°，
∴∠AEC=180°-∠A-∠ACE=72°，
∴∠A=∠AEC，∠B=∠ECB，
∴CA=CE，CE=BE，
∴AC=EC=BE=1，设AE=x，
∵∠ACE=∠B，∠A=∠A，
∴△ACE∽△ABC，
∴$\frac{AC}{AB}$=$\frac{AE}{AC}$，
∴$\frac{1}{1+x}$=$\frac{x}{1}$，
∴x²+x-1=0，
∴x=$\frac{-1+\sqrt{5}}{2}$或$\frac{-1-\sqrt{5}}{2}$（舍弃），
∴AB=BE+AE=1+$\frac{-1+\sqrt{5}}{2}$=$\frac{\sqrt{5}+1}{2}$，
∵∠A=∠ACB=72°，
∴BC=AB=$\frac{\sqrt{5}+1}{2}$，
∴c=$\frac{\sqrt{5}+1}{2}$，
故答案为$\frac{\sqrt{5}+1}{2}$．

（2）过点A作∠BAC的平分线交BC于D，作DE⊥AB于E，DF⊥AC于F．
设BD=x，则CD=6-x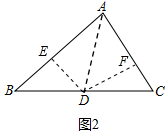

∵∠CAB=2∠B，∠CAD=∠DAB，
∴∠CAD=∠B，∵∠C=∠C，
∴△CAD∽△CBA，
∴$\frac{CD}{AC}$=$\frac{AC}{BC}$，
∴$\frac{6-x}{4}$=$\frac{4}{6}$，
∴x=$\frac{10}{3}$，
∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F
∴点DE=DF，
∵$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$=$\frac{\frac{1}{2}•AB•DE}{\frac{1}{2}•AC•DF}$=$\frac{AB}{AC}$
∴$\frac{\frac{10}{3}}{\frac{8}{3}}$=$\frac{AB}{4}$
∴AB=5，即c=5．

（3）过点A作AD平分∠BAC交BC于D，过点A作∠DAC的平分线交CD于E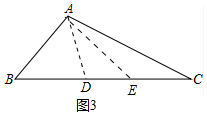

∵∠A=2∠B=4∠C，
∴∠B=∠DAB=∠AEC，
∴DA=DB，AB=AE=EC=c
设DB=DA=x，则DE=a-c-x
∵∠ADE=∠ADC，∠DAE=∠C，
∴△ADE∽△CAB
∴$\frac{DE}{AB}$=$\frac{AD}{AC}$，
即$\frac{a-c-x}{c}$=$\frac{x}{b}$     ①
由（2）同理可得，$\frac{AD}{AC}$=$\frac{DE}{CE}$，
即$\frac{x}{c}$=$\frac{a-x}{b}$         ②
由①+②可得，$\frac{a-c}{c}$=$\frac{a}{b}$，
∴$\frac{a}{c}$-1=$\frac{a}{b}$，
∴$\frac{a+b}{b}$=$\frac{a}{c}$，
∴$\frac{a+b}{ab}$=$\frac{1}{c}$=$\frac{1}{3}$．

点评 本题考查三角形综合题、相似三角形的判定和性质、角平分线、方程组等知识，解题的关键是学会利用面积法，推得$\frac{AB}{AC}$=$\frac{BD}{DC}$，学会利用参数解决问题，属于中考压轴题．