
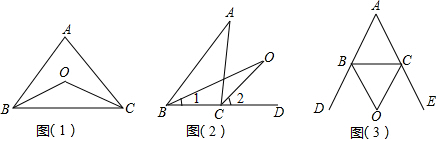
���� ��1��̽��1�����ݽ�ƽ���ߵĶ���ɵá�OBC=$\frac{1}{2}$��ABC����OCB=$\frac{1}{2}$��ACB��Ȼ���ʾ����OBC+��OCB���ٸ��������ε��ڽǺ͵���180����ʽ�������ɣ�
̽��2�����ý�ƽ���ߵ���������ǵ����ʵó���2=$\frac{1}{2}$��A+��1����BOC=��2-��1��Ȼ���������ɵõ���BOC���A�Ĺ�ϵ��
̽��3�����������ε�һ����ǵ������������ڵ������ڽǵĺ��Լ���ƽ���ߵĶ����ʾ����OBC���OCB��Ȼ���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣮
��2���ɣ�1����̽���ɵó����ۣ�
��� �⣺��1��̽��1�����ۣ���BOC=90��+$\frac{1}{2}$��A��
���ɣ��ߡ�ABC���ACB��ƽ�����ཻ�ڵ�O��
���OBC=$\frac{1}{2}$��ABC����OCB=$\frac{1}{2}$��ACB��
���OBC+��OCB=$\frac{1}{2}$����ABC+��ACB����
�ڡ�OBC�У���BOC=180��-����OBC+��OCB��
=180��-$\frac{1}{2}$����ABC+��ACB��
=180��-$\frac{1}{2}$��180��-��A��
=90��+$\frac{1}{2}$��A��
ͨ����������̽��2���ۣ���BOC=90��+$\frac{1}{2}$��A��
�������£���BO��CO�ֱ��ǡ�ABC�͡�ACB�Ľ�ƽ���ߣ�
���1=$\frac{1}{2}$��ABC����2=$\frac{1}{2}$��ACB��
���1+��2=$\frac{1}{2}$����ABC+��ACB����
�֡ߡ�ABC+��ACB=180��-��A��
���1+��2=$\frac{1}{2}$��180��-��A��=90��-$\frac{1}{2}$��A��
���BOC=180��-����1+��2����
=180��-��90��-$\frac{1}{2}$��A����
=90��+$\frac{1}{2}$��A��
̽��2���ۣ���BOC=$\frac{1}{2}$��A��
�������£�
��BO��CO�ֱ��ǡ�ABC�͡�ACD�Ľ�ƽ���ߣ�
���1=$\frac{1}{2}$��ABC����2=$\frac{1}{2}$��ACD��
�֡ߡ�ACD�ǡ�ABC��һ��ǣ�
���ACD=��A+��ABC��
���2=$\frac{1}{2}$����A+��ABC��=$\frac{1}{2}$��A+��1��
�ߡ�2�ǡ�BOC��һ��ǣ�
���BOC=��2-��1=$\frac{1}{2}$��A+��1-��1=$\frac{1}{2}$��A��
̽��3���ۣ���BOC=90��-$\frac{1}{2}$��A��
���ɣ��ߡ�OBC=$\frac{1}{2}$����A+��ACB������OCB=$\frac{1}{2}$����A+��ABC����
���BOC=180��-��0BC-��OCB��
=180��-$\frac{1}{2}$����A+��ACB��-$\frac{1}{2}$����A+��ABC����
=180��-$\frac{1}{2}$��A-$\frac{1}{2}$����A+��ABC+��ACB����
���BOC=90��-$\frac{1}{2}$��A��
�ʴ�Ϊ����BOC=90��+$\frac{1}{2}$��A����BOC=90��+$\frac{1}{2}$��A����BOC=90��-$\frac{1}{2}$��A��
��2��ѡ��̽��1��֤������ͬ��1����
���� ���⿼���������ε�����������ڽǺͶ�������������ε�һ����ǵ������������ڵ������ڽǵĺ��ǽ���Ĺؼ���������Ŀ�ṩ����Ϣ��Ȼ�������ṩ��Ϣ��˼·Ҳ����Ҫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
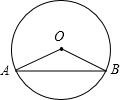 ��1����ͼ����AB�ѡ�O�ֳ�2��7����AOB=80�㣻
��1����ͼ����AB�ѡ�O�ֳ�2��7����AOB=80�㣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڳ�����ABCD�У�AD=8cm��CD=4cm��
��ͼ���ڳ�����ABCD�У�AD=8cm��CD=4cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬��D��AC�ϣ���DE��AB������Ϊ��E�����B=��ADE
��ͼ���ڡ�ABC�У���ACB=90�㣬��D��AC�ϣ���DE��AB������Ϊ��E�����B=��ADE�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com