
分析 根据一元二次方程的定义,一元二次方程必须满足两个条件:未知数的最高次数是2;二次项系数不为0.由这两个条件得到相应的关系式,再求解即可.
解答 解:(1)x2-9=0是一元二次方程;
(2)(x+3)(x-1)=x2是一元一次方程;
(3)(2x+1)(2x-1)=0是一元二次方程;
(4)$\frac{1}{3x}$-y2=0是分式方程;
(5)x2=0是一元二次方程;
(6)$\sqrt{{x}^{2}-2x+1}$=1是无理方程.
点评 本题利用了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,MN是⊙O的直径.
如图,MN是⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
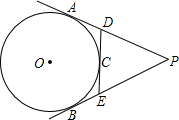 如图,PA、PB分别切⊙O于A、B两点,过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E.求证:∠DOE=90°-$\frac{1}{2}$∠P.
如图,PA、PB分别切⊙O于A、B两点,过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E.求证:∠DOE=90°-$\frac{1}{2}$∠P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com