
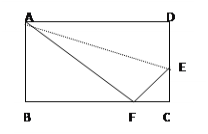
【题目】如图,矩形ABCD中,折叠矩形一边AD,使点D落在BC边的点F处,已知折痕AE=![]() ,且CE:CF=3:4,则矩形ABCD的周长为()
,且CE:CF=3:4,则矩形ABCD的周长为()
A. 36cm B. 3![]() C. 72cm D. 7
C. 72cm D. 7![]()
【答案】C
【解析】
由CE:CF=3:4.在Rt△EFC中可设CF=4k,EF=DE=5k,根据∠BAF=∠EFC,利用相似三角形的性质求出AF,然后在Rt△AEF中利用勾股定理求出k,继而代入可得出答案.
设CE=3k,则CF=4k,由勾股定理得:EF=DE=5k,∴DC=AB=8k.
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,∴∠BAF=∠EFC.
∵∠B=∠C=90°,∴△ABF∽△FCE,∴AB:BF=FC:CE=4:3,∴BF=6k,AF=BC=AD=10k.在Rt△AFE中由勾股定理得:![]() ,解得:k=2,则矩形ABCD的周长=2(AB+BC)=2(8k+10k)=72(cm).
,解得:k=2,则矩形ABCD的周长=2(AB+BC)=2(8k+10k)=72(cm).
故选C.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
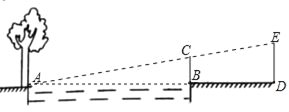
【题目】如图,洋洋和华华用所学的数学知识测量一条小河的宽度,河的对岸有一棵大树,底部记为点A,在他们所在的岸边选择了点B,并且使AB与河岸垂直,在B处与地面垂直竖起标杆BC,再在AB的延长线上选择点D,与地面垂直竖起标杆DE,使得A、C、E三点共线.经测量,BC=1m,DE=1.5m,BD=5m,求小河的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
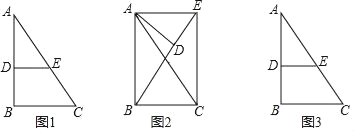
【题目】(1)观察发现:如图1,在Rt△ABC中,∠B=90°,点D在边AB上,过D作DE∥BC交AC于E,AB=5,AD=3,AE=4.填空:
①△ABC与△ADE是否相似?(直接回答) ;
②AC= ;DE= .
(2)拓展探究:将△ADE绕顶点A旋转到图2所示的位置,猜想△ADB与△AEC是否相似?若不相似,说明理由;若相似,请证明.
(3)迁移应用:将△ADE绕顶点A旋转到点B、D、E在同一条直线上时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
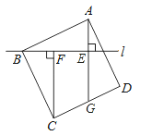
【题目】如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
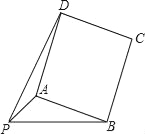
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
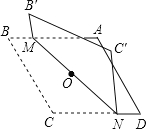
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解飞行员视力的达标率应使用抽样调查
B.一组数据3,6,6,7,9的中位数是6
C.从2000名学生中选200名学生进行抽样调查,样本容量为2000
D.一组数据1,2,3,4,5的方差是10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com