
以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
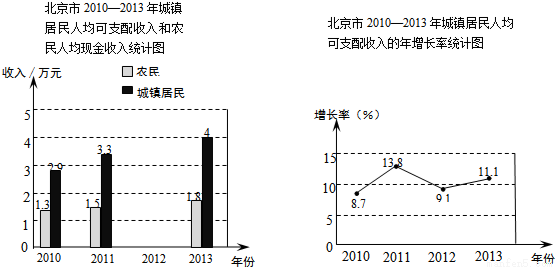
根据以上信息,解答下列问题:
(1)2012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,则2012年农民人
均现金收入是 万元,请根据以上信息补全条形统计图,并标明相应的数据(结果精确到0.1);
(2)在2010—2013年这四年中,北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年
份是 年;
(3)①2011—2013年城镇居民人均可支配收入的年平均增长率最接近 ;
A.14% B.11% C.10% D.9%
②若2014年城镇居民人均可支配收入按①中的年平均增长率增长,请预测2014年的城镇居民人均可支配收入为 万元(结果精确到0.1).
(1)1.6;(2)2013;(3)①B;②4.4.
【解析】
试题分析:(1)利用条形统计图得出2011年城镇居民人均可支配收入为3.3万元,进而得出2012年农民人均现金收入.
(2)利用折线条求出2012年城镇居民人均可支配收入,进而分别求出各年份的城镇居民人均可支配收入和农民人均现金收入相差数额进而得出答案.
根据2011年以及2013年城镇居民人均可支配收入进而得出等式方程求出即可;
②利用①中所求直接求出2014年的城镇居民人均可支配收入即可.
试题解析:(1)∵由条形图可得出:2011年城镇居民人均可支配收入为3.3万元,
2012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,
∴2012年农民人均现金收入是:3.3÷2-0.05=1.6(万),
(2)∵2011年到2012年城镇居民人均可支配收入增长率为9.1%,
∴2012年人均可支配收入为:3.3×(1+9.1%)≈3.6(万元),
∵2.9-1.3=1.6(万),3.3-1.5=1.8(万),3.6-1.6=2(万),4-1.8=2.2(万),
∴在2010-2013年这四年中,北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年份是2013年;
(3)①设2011-2013年城镇居民人均可支配收入的年平均增长率为x,则
3.3(1+x)2=4,
解得:x1≈-2.1(不合题意舍去),x2≈0.11=11%.
故选B.
②由①得:2014年的城镇居民人均可支配收入为:4×(1+11%)=4.4(万).
考点:1.折线统计图;2.条形统计图;3.一元二次方程的应用(增长率问题).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:解答题
设 ,
, 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式 ≤
≤ ≤
≤ 的实数
的实数 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为 . 对于一个函数,如果它的自变量
. 对于一个函数,如果它的自变量 与函数值
与函数值 满足:当m≤
满足:当m≤ ≤n时,有m≤
≤n时,有m≤ ≤n,我们就称此函数是闭区间
≤n,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的表达式;
上的“闭函数”,求此函数的表达式;
(3)若二次函数 是闭区间
是闭区间 上的“闭函数”,直接写出实数
上的“闭函数”,直接写出实数 ,
, 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:选择题
已知⊙ 的半径为1cm,⊙
的半径为1cm,⊙ 的半径为3cm,两圆的圆心距
的半径为3cm,两圆的圆心距 为4cm,则两圆的位置关系是( )
为4cm,则两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道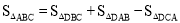 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系 中,以点A(2,3)为顶点任作一直角∠PAQ,使其两边分别与x轴、y轴的正半轴交于点P、Q,连接PQ,过点A作AH⊥PQ于点H,设点P的横坐标为x,AH的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
中,以点A(2,3)为顶点任作一直角∠PAQ,使其两边分别与x轴、y轴的正半轴交于点P、Q,连接PQ,过点A作AH⊥PQ于点H,设点P的横坐标为x,AH的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是 ;,
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com