
在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是 ;,
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).

(1)BE= CD;(2)BE=
CD;(2)BE= CD;(3)BE=2CD·sinα,证明见解析.
CD;(3)BE=2CD·sinα,证明见解析.
【解析】
试题分析:(1)由已知,△ADE和△ACB都是等腰直角三角形,所以有AE= AD,AB=
AD,AB= AC,从而有
AC,从而有 ,即BE=
,即BE= CD.
CD.
(2)如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=120°,
∴∠CAB=∠DAE,∠ACM=∠ADN=60° ,AM= AB,AN=
AB,AN= AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM= =
= ,sin∠ADN=
,sin∠ADN= =
= ,
,
∴ .∴
.∴ .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴ .∴BE=
.∴BE= CD.
CD.

(3)根据等腰三角形的性质和锐角三角函数定义求得 ,再由△BAE∽△CAD得出
,再由△BAE∽△CAD得出 ,从而得出结论.
,从而得出结论.
(1)BE= CD.
CD.
(2)BE= CD.
CD.
(3)BE=2CD·sinα.证明如下:
如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=2α ,
∴∠CAB=∠DAE,∠ACM=∠ADN=α ,AM= AB,AN=
AB,AN= AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM= ,sin∠ADN=
,sin∠ADN= ,
,
∴ .∴
.∴ .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴ .
.
∴BE=2DC·sinα.

考点:1.旋转问题;2.等腰(直角)三角形的性质;3.锐角三角函数定义;4.相似三角形的判定和性质.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
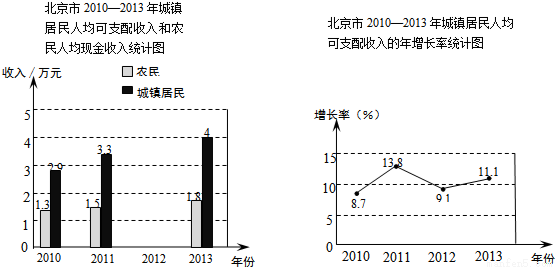
根据以上信息,解答下列问题:
(1)2012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,则2012年农民人
均现金收入是 万元,请根据以上信息补全条形统计图,并标明相应的数据(结果精确到0.1);
(2)在2010—2013年这四年中,北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年
份是 年;
(3)①2011—2013年城镇居民人均可支配收入的年平均增长率最接近 ;
A.14% B.11% C.10% D.9%
②若2014年城镇居民人均可支配收入按①中的年平均增长率增长,请预测2014年的城镇居民人均可支配收入为 万元(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:填空题
如图,矩形台球桌ABCD的尺寸为2.7m 1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.
1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:选择题
一个不透明的盒子中放有4个白色乒乓球和2个黄色乒乓球,所有乒乓球除颜色外完全相同,从中随机摸出1个乒乓球,摸出黄色乒乓球的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
如图,△ABC中,BC >AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:填空题
如图,在反比例函数 (x > 0)的图象上有点A1,A2,A3,…,An-1,An ,这些点的横坐标分别是1,2,3,…,n -1,n时,点A2的坐标是__________;过点A1 作x轴的垂线,垂足为B1,再过点A2作A2 P1⊥A1 B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2 A2A3,…,△P n-1 An-1 An,其面积分别记为S2,…,Sn-1,则S1+ S2+…+ Sn=________.
(x > 0)的图象上有点A1,A2,A3,…,An-1,An ,这些点的横坐标分别是1,2,3,…,n -1,n时,点A2的坐标是__________;过点A1 作x轴的垂线,垂足为B1,再过点A2作A2 P1⊥A1 B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2 A2A3,…,△P n-1 An-1 An,其面积分别记为S2,…,Sn-1,则S1+ S2+…+ Sn=________.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
【小题1】求证:BC=CD;
【小题2】求证:∠ADE=∠ABD;
【小题3】设AD=2,AE=1,求⊙O直径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com