搜索
【题目】如图，将ABCD沿对角线AC折叠，使点B落在点B'处．若∠1=∠2=44°，则∠B的大小为度．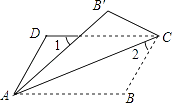
参考答案：
【答案】114
【解析】解：在ABCD中，AB∥CD，
∴∠BAB′=∠1=44°，
∵ABCD沿对角线AC折叠，使点B落在点B'处，
∴∠BAC=∠B′AC，
∴∠BAC= 
∠BAB′= ×44°=22°，
在△ABC中，∠B=180°﹣∠BAC﹣∠2=180°﹣22°﹣44°=114°．
所以答案是：114．
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OABC的对角线OB、AC相交于点D，BE∥AC，AE∥OB．函数
（k＞0，x＞0）的图象经过点E．若点A、C的坐标分别为（3，0）、（0，2），则k的值为（ ）
A.3
B.4
C.4.5
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，BC=9，AC=12．分别以点A和点B为圆心、大于AB一半的长为半径作圆弧，两弧相交于点E和点F，作直线EF交AB于点D，连结CD．则CD的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，从点
... 依次扩展下去，则 
的坐标为 ( ) 
A. (505,-505)B. (-505,505)C. (-505,504)D. (-506,505)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系xoy中，已知A（6，0），B（8，6），将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD．
（1）写出点C的坐标；
（2）当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；
（3）设∠OCD=α，∠DBA=β，∠BDC=θ，判断α、β、θ之间的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，以边AB上的一点O为圆心，以OA的长为半径的圆交边AB于点D，BC与⊙O相切于点C．若⊙O的半径为5，∠A=20°，则
的长为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在直角坐标系中。
（1）请写出△ABC各点的坐标；
（2）求出△ABC的面积S△ABC；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A1B1C1，在图中画出△A1B1C1，并写出△A1B1C1的坐标。
相关试题
