
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC=6,∠B=60°,∠D=90°,连结AC.动点P从点B出发,沿BC以每秒1个单位的速度向终点C运动(点P不与点B、C重合).过点P作PQ⊥BC交AB或AC于点Q,以PQ为斜边作Rt△PQR,使PR∥AB.设点P的运动时间为t秒.
(1)当点Q在线段AB上时,求线段PQ的长.(用含t的代数式表示)
(2)当点R落在线段AC上时,求t的值.
(3)设△PQR与△ABC重叠部分图形的面积为S平方单位,求S与t之间的函数关系式.
(4)当点R到C、D两点的距离相等时,直接写出t的值.
【答案】
(1)解:如图1中,

当点Q在线段AB上时,BP=t,
在Rt△PQB中,∵∠BPQ=90°,∠B=60°,
∴PQ=BPtan60°= ![]() t(0<t≤3)
t(0<t≤3)
(2)解:如图2中,

当R落在AC上时,易知PC=RC=PQ,
在Rt△PQR中,∵∠PRQ=90°,PQ= ![]() t,∠PQR=60°,
t,∠PQR=60°,
∴PR=PQsin60°= ![]() t,
t,
由BP+PC=6可得,t+ ![]() t=6,
t=6,
解得t= ![]() s
s
(3)解:如图3中.当0<t≤ ![]() 时,重叠部分是△PQR.
时,重叠部分是△PQR.

S= ![]() QRPR=
QRPR= ![]()
![]() t
t ![]() t=
t= ![]() t2.
t2.
如图4中,当 ![]() <t≤3时,重叠部分是四边形PMNQ.
<t≤3时,重叠部分是四边形PMNQ.

S=S△PQR﹣S△RMN= ![]() t2﹣
t2﹣ ![]() [
[ ![]() t﹣(6﹣t)]
t﹣(6﹣t)] ![]() [
[ ![]() t﹣(6﹣t)]=﹣
t﹣(6﹣t)]=﹣ ![]() t2+15
t2+15 ![]() t﹣18
t﹣18 ![]() .
.
如图5中,当3<t<6时,重叠部分是△PQM.

S= ![]() S△PQC=
S△PQC= ![]()
![]() (6﹣t)
(6﹣t) ![]() (6﹣t)=
(6﹣t)= ![]() t2﹣3
t2﹣3 ![]() t+9
t+9 ![]()
(4)解:在图3中,点R到C、D两点的距离相等时,则有 ![]() tsin60°=
tsin60°= ![]() ×6×
×6× ![]() ,解得t=2.
,解得t=2.
在图5中,点R到C、D两点的距离相等时,则有 ![]() (6﹣t)
(6﹣t) ![]() =
= ![]() 6
6 ![]() ,解得t=4.
,解得t=4.
综上所述,t=2s或4s时,点R到C、D两点的距离相等
【解析】(1)Rt△PQB中利用解直角三角形易求出线段PQ的长。
(2)当R落在AC上时,易知PC=RC=PQ,在Rt△PQR中,利用解直角三角形求出PR= 3 2 t,由BP+PC=6,建立方程求出t的值。
(3)分三种情况进行讨论:如图3中.当0<t≤ ![]() 时,重叠部分是△PQR.根据三角形的面积公式,可求出S与t之间的函数关系式;如图4中,当
时,重叠部分是△PQR.根据三角形的面积公式,可求出S与t之间的函数关系式;如图4中,当 ![]() <t≤3时,重叠部分是四边形PMNQ,根据S=S△PQR﹣S△RMN即可求出结果;如图5中,当3<t<6时,重叠部分是△PQM.则S=
<t≤3时,重叠部分是四边形PMNQ,根据S=S△PQR﹣S△RMN即可求出结果;如图5中,当3<t<6时,重叠部分是△PQM.则S= ![]() S△PQC,即可求出S与t之间的函数关系式。
S△PQC,即可求出S与t之间的函数关系式。
(4)根据两种情况在图3和图5中,根据点R到C、D两点的距离相等建立方程求解即可。
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图,三个村庄A,B,C之间的距离分别为![]() ,已知A,B两村之间已修建了一条笔直的村级公路AB,为了实现村村通公路,现在要从C村修一条笔直公路CD直达AB,已知公路的造价为10000元/km,则修这条公路的最低造价是多少元?
,已知A,B两村之间已修建了一条笔直的村级公路AB,为了实现村村通公路,现在要从C村修一条笔直公路CD直达AB,已知公路的造价为10000元/km,则修这条公路的最低造价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)【参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书本数相等.
(1)求去年购买的文学书和科普书的单价各是多少元?
(2)若今年文学书的单价比去年提高了![]() ,科普书的单价与去年相同,为了普及科普知识,书店举办了每买三本科普书就赠一本文学书的优惠活动,这所中学今年计划在优惠活动期间,再购进文学书和科普书共200本,且购买文学书和科普书的总费用不超过1880元,这所中学今年最多能购进多少本文学书?
,科普书的单价与去年相同,为了普及科普知识,书店举办了每买三本科普书就赠一本文学书的优惠活动,这所中学今年计划在优惠活动期间,再购进文学书和科普书共200本,且购买文学书和科普书的总费用不超过1880元,这所中学今年最多能购进多少本文学书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济宁市“五城同创”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作:然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,①第七次操作共得到个三角形;②若要得到220个小三角形,则需要操作的次数是 . 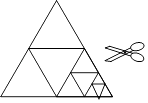
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com