
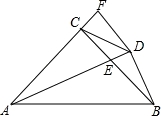
如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )
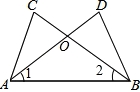
A.AC=BD B.∠1=∠2 C.AD=BC D.∠C=∠D
C【考点】全等三角形的判定.
【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.
【解答】解:A、∵AC=BD,∠CAB=∠DBA,AB=AB,
∴根据SAS能推出△ABC≌△BAD,故本选项错误;
B、∵∠CAB=∠DBA,AB=AB,∠1=∠2,
∴根据ASA能推出△ABC≌△BAD,故本选项错误;
C、根据AD=BC和已知不能推出△ABC≌△BAD,故本选项正确;
D、∵∠C=∠D,∠CAB=∠DBA,AB=AB,
∴根据AAS能推出△ABC≌△BAD,故本选项错误;
故选C.
【点评】本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有 SAS,ASA,AAS,SSS.
SAS,ASA,AAS,SSS.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9.
(1)求CD的长为__________.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
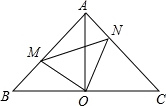
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A,D重合,记PB+PC=a,AB+AC=b,则a,b的大小关系是( )
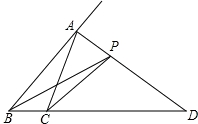
A.a>b B.a=b C.a<b D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①∠ADC=45°;②BD=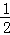 AE;③AC+CE=AB;④AB﹣BC=2FC;其中正确的结论有( )
AE;③AC+CE=AB;④AB﹣BC=2FC;其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com