
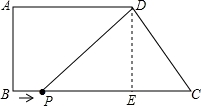
如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9.
(1)求CD的长为__________.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?

【考点】勾股定理;等腰三角形的判定.
【专题】动点型.
【分析】(1)过点D作DE⊥BC,垂足为E,先判断出四边形ABED是矩形,在Rt△DCE中根据勾股定理即可得出CD的长;
(2)过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.再分CD=CP,CD=PD,PD=PC三种情况进行讨论.
【解答】解:(1)过点D作DE⊥BC,垂足为E,
∵AD∥BC,∠B=90°,
∴四边 形ABED是矩形,
形ABED是矩形,
∴BE=AD=6,DE=AB=4,
∴CE=BC﹣BE=9﹣6=3,
在Rt△DCE中,CD=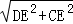 =
=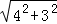 =5.
=5.
故答案为:5;
(2)过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.
当CD=CP时,5=9﹣t,解得t=4;
当CD=PD时,E为PC中点,
∴6﹣t=3,
∴t=3;
当PD=PC时,PD2=PC2,
∴(6﹣t)2+42=(9﹣t)2,
解得t=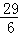 .
.
故t的值为t=3或4或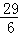 .
.
【点评】本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:
△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=( )

A.110° B.120° C.130° D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料:x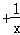 =c
=c 的解是x1=c,x2=
的解是x1=c,x2= ;
;
x﹣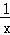 =c﹣
=c﹣ (即x
(即x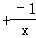 =c
=c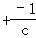 的解是x1=c,x2=﹣
的解是x1=c,x2=﹣ ;
;
x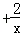 =c
=c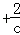 的解是x1=c,x2=
的解是x1=c,x2=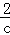 ;
;
x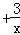 =c
=c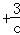 的解是x1=c,x2=
的解是x1=c,x2=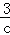 ;
;
…
(1)请观察上述方程与解的特征,猜想方程x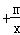 =c
=c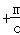 (m≠0)的解,并验证你的结论.
(m≠0)的解,并验证你的结论.
(2)利用这个结论解关于x的方程:x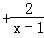 =a
=a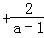 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
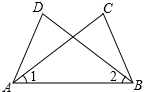
如图,已知∠1=∠2,要说明△ABC≌△BAD,
(1)若以“SAS”为依据,则需添加一个条件是__________;
(2)若以“ASA”为依据,则需添加一个条件是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;
(2)在直线l上找一点P(在答题纸上图中标出),使PB+PC的长最短,这个最短长度的平方值是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com