
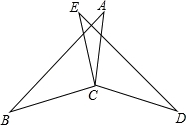
如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
对于任意三角形的高,下列说法不正确的是( )
A.锐角三角形有三条高
B.直角三角形只有一条高
C.任意三角形都有三条高
D.钝角三角形有两条高在三角形的外部
查看答案和解析>>
科目:初中数学 来源: 题型:
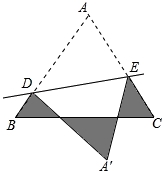
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9.
(1)求CD的长为__________.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
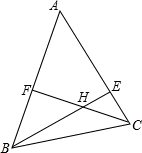
如图,已知BE,CF分别为△ABC的两条高,BE和CF相交于点H,若∠BAC=50°,则∠BHC为( )
A.160° B.150° C.140° D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
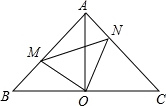
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com