
如图,已知∠1=∠2,要说明△ABC≌△BAD,
(1)若以“SAS”为依据,则需添加一个条件是__________;
(2)若以“ASA”为依据,则需添加一个条件是__________.
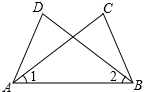
(1) AD=BC;
(2) ∠ABC=∠BAD.
【考点】全等三角形的判定.
【分析】(1)添加AD=BC,再加上条件∠1=∠2,AB=BA可利用SAS判定△ABC≌△BAD;
(2)添加∠ABC=∠BAD,再加上条件∠1=∠2,AB=BA可利用ASA判定△ABC≌△BAD.
【解答】解:(1)添加AD=BC,
∵在△ABC和△BAD中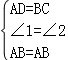 ,
,
∴△ABC≌△BAD(SAS);
故答案为:AD=BC;
(2)添加∠ABC=∠BAD,
∵在△ABC和△BAD中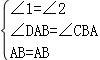 ,
,
∴△ABC≌△BAD(ASA),
故答案为:∠ABC=∠BAD.
【点评】此题主要考查了全等三角形的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9.
(1)求CD的长为__________.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知BE,CF分别为△ABC的两条高,BE和CF相交于点H,若∠BAC=50°,则∠BHC为( )
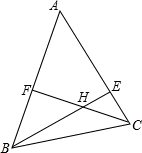
A.160° B.150° C.140° D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
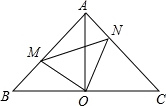
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com