
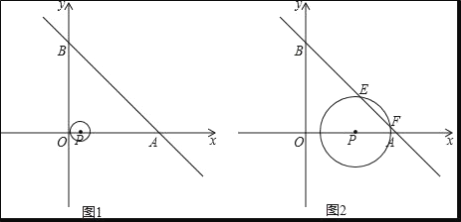
【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=![]() 时,弦EF的长;
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
【答案】(1)(10,0),(0,10),45°.(2)(1+2t,0),1+t.(3)![]() .
.
【解析】试题分析:(1)利用待定系数法求出点A、B的坐标,即可解决问题.
(2)根据题意可得P(1+2t,0),⊙O半径为1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.在Rt△APK中,由∠PKA=90°,∠PAK=45°,PA=4,推出PK=![]() PA=2
PA=2![]() ,在Rt△PEK中,根据EK=
,在Rt△PEK中,根据EK=![]() 计算即可.
计算即可.
②分两种情形a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°;b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.分别列出方程求解即可.
试题解析:
解:(1)∵y=﹣x+10的图象交x轴于点A,交y轴于点B,
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0),⊙O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
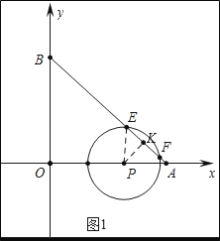
当t=![]() 时,P(6,0),半径为3.5,
时,P(6,0),半径为3.5,
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=![]() ,PA=2
,PA=2![]() ,
,
在Rt△PEK中,EK=![]() =
=![]() ,
,
∴EF=2EK=![]() .
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°
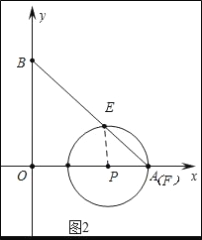
∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=![]() .
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
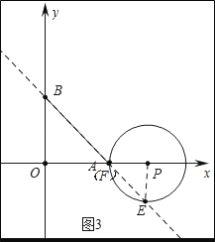
由OP﹣PF=OA,
∴1+2t﹣(1+t)=10,
∴t=10,
综上所述,t=![]() s或10s时,存在以点P为直角顶点的Rt△PEF.
s或10s时,存在以点P为直角顶点的Rt△PEF.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF,现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当边CD′恰好经过EF的中点H时,求旋转角α的大小;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△BCD′能否全等?若能,直接写出旋转角α的大小;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
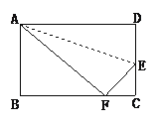
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).
(1)求BF的长;(2)求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作![]() ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.

(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
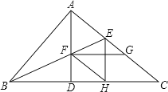
A.①②③④ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
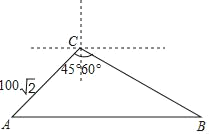
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).
(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com