练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，BC=BD，AD=AE，DE=CE，∠A=36°，则∠B=( )

    A. 45B. 36°C. 72°D. 30°

    【答案】B

    【解析】

    由AD=AE，∠A=36°，根据等腰三角形的性质及三角形的内角和定理，即可求得∠ADE的度数；又由三角形外角的性质，即可求得∠CED的度数；由DE=CE，求得∠EDC的度数，然后根据平角的定义求得∠BDC的度数，又由BC=BD，即可求得∠B的值．

    ∵AD=AE，∠A=36°，

    ∴∠ADE=∠AED==72°，

    ∴∠DEC=∠A+∠ADE=36°+72°=108°，

    ∵DE=CE，

    ∴∠EDC=∠ECD==36°，

    ∴∠CDB=180°-∠ADE-∠EDC=72°，

    ∵BC=BD，

    ∴∠BCD=∠CDB=72°，

    ∴∠B=180°-∠BCD-∠CDB=36°．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，□ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，AB＝4，则□ABCD的面积等于________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司计划购买A、B两种计算器共100个，要求A种计算器数量不低于B种的，且不高于B种的．已知A、B两种计算器的单价分别是150元/个、100元/个，设购买A种计算器x个．

    （1）求计划购买这两种计算器所需费用y（元）与x的函数关系式；

    （2）问该公司按计划购买者两种计算器有多少种方案？

    （3）由于市场行情波动，实际购买时，A种计算器单价下调了3m（m＞0）元/个，同时B种计算器单价上调了2m元/个，此时购买这两种计算器所需最少费用为12150元，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场统计了今年1～5月A，B两种品牌冰箱的销售情况，并将获得的数据绘制成折线统计图

    （1）该商场这段时间内A.B两种品牌冰箱月销售量的中位数分别为 ， ；

    （2）计算两种品牌月销售量的方差，比较并说明该商场1～5月这两种品牌冰箱月销售量的稳定性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．

    根据以上信息解决下列问题：

    （1） ， ；

    （2）扇形统计图中机器人项目所对应扇形的圆心角度数为 ；

    （3）从选航模项目的名学生中随机选取名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的名学生中恰好有名男生、名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）当a≠0时，求的值．（写出解答过程）

    （2）若a≠0，b≠0，且+ =0，则的值为　 　．

    （3）若ab＞0，则++的值为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图本题图①，在等腰Rt中， ,，为线段上一点，以为半径作交于点,连接、，线段、、的中点分别为、、.

    （1）试探究是什么特殊三角形？说明理由；

    （2）将绕点逆时针方向旋转到图②的位置，上述结论是否成立？并证明结论；

    （3）若,把绕点在平面内自由旋转，求的面积y的最大值与最小值的差.

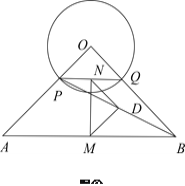
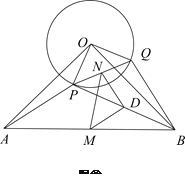
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．

    （1）BD与CD有什么数量关系，并说明理由；

    （2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，在△ABC中，∠B＜∠C，AD，AE分别是△ABC的高和角平分线，

    （1）若∠B＝30°，∠C＝50°．则∠DAE的度数是　 　．（直接写出答案）

    （2）写出∠DAE、∠B、∠C的数量关系：　 　，并证明你的结论．

    查看答案和解析>>

    同步练习册答案