
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
![]()
【答案】8
【解析】
解决此类问题的关键在于将新运算转化为学过的数的有关运算法则进行计算,从而求出答案.
本题提供的“F运算”,需要对正整数n分情况(奇数、偶数)循环计算,由于n=449为奇数应先进行F①运算,即3×449+5=1352 (偶数),需再进行F②运算,即1352÷23=169 (奇数),再进行F①运算,得到3×169+5=512 (偶数),再进行F②运算,即512÷29=1 (奇数),再进行F①运算,得到3×1+5=8 (偶数),再进行F②)运算,即8÷23=1,再进行F①运算得到3×1+5= 8(偶数),.,即第1次运算结果为1352,...第4次运算结果为1,第5次运算结果为8,…可以发现第6次运算结果为1,第7次运算结果为8,从第6次运算结果开始循环,且奇数次运算的结果为8,偶数次为1,而第499次是奇数,这样循环计算一直到第449次“F运算”,得到的结果为8,故本题答案为:8.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
⑴试说明:BE=CF;
⑵若AF=3,BC=4,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次军事演习中,蓝方在﹣条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
(1)求点C到公路的距离;
(2)求红蓝双方最初的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC.
(1)用直尺和圆规作∠A的平分线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() ;
;
(要求:不写作法,但需要保留画图痕迹)
(2)设(1)中的![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请你探究BE和CF之间的数量关系,并加以证明.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请你探究BE和CF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB在平面直角坐标系中,点O与坐标原点重合,点A在x轴上,点B在y轴上,![]() ,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
,将△AOB沿直线BE折叠,使得OB边落在AB上,点O与点D重合.
(1)求直线BE的解析式;
(2)求点D的坐标;
(3)x轴上是否存在点P,使△PAD为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(﹣1,0),有以下结论:①abc>0;②4a﹣2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(﹣3,y1)(﹣6,y2)都在抛物线上,则y1<y2 . 其中正确的是 . (只填序号) 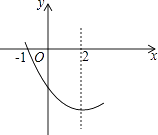
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N. 
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com