
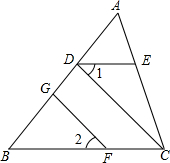
 如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由.
如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由. 分析 CD⊥AB.理由:先由∠ADE=∠B,根据同位角相等两直线平行,可得:DE∥BC,然后根据两直线平行内错角相等,可得∠1=∠DCB,然后由∠2=∠1,根据等量代换可得:∠2=∠DCB,然后根据同位角相等两直线平行可得:DC∥GF,然后根据两直线平行同位角相等可得:∠CDB=∠FGB,然后由GF⊥AB,可得:∠CDB=90°,进而可得:∠FGB=90°,然后根据垂直的定义可得:CD⊥AB.
解答 解:CD⊥AB.
理由:∵∠ADE=∠B,
∴DE∥BC,
∴∠1=∠DCB,
∵∠2=∠1,
∴∠2=∠DCB,
∴DC∥GF,
∴∠CDB=∠FGB,
∵GF⊥AB,
∴∠CDB=90°,
∴∠FGB=90°,
∴CD⊥AB.
点评 此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等?两直线平行;内错角相等?两直线平行;同旁内角互补?两直线平行.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
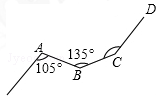 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角∠A是105度,第二次拐的角∠B是135度,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C=150°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 3 | 4 | x |
| -2 | y | a |
| 2y-x | c | b |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
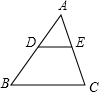 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=9,$\frac{AD}{BD}$=$\frac{3}{4}$,则EC的长是
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=9,$\frac{AD}{BD}$=$\frac{3}{4}$,则EC的长是| A. | 4.5 | B. | 8 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
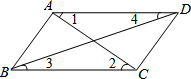 如图所示,下列四组条件中,不能判定AD∥BC的是( )
如图所示,下列四组条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ABC=∠ADC | D. | ∠BAD+∠ABC=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com