
【题目】如图,在平面直角坐标系中,直线![]() 与双曲线
与双曲线![]() 交于第一、三象限内的
交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() ,
,![]() ,点
,点![]() 的纵坐标为4.
的纵坐标为4.

(1)求反比例函数和一次函数的函数表达式;
(2)连接![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)在(1)的条件下,根据图像直接写出反比例函数的值小于一次函数的值时,自变量![]() 的取值范围.
的取值范围.
【答案】(1)反比例函数解析式为![]() ;一次函数解析式为
;一次函数解析式为![]() ;(2)4;
;(2)4;
(3)![]() 或
或![]() .
.
【解析】
(1)根据BM⊥![]() 轴,可知△BMO为等腰直角三角形,可求得点B的坐标,将其代入反比例函数,求出
轴,可知△BMO为等腰直角三角形,可求得点B的坐标,将其代入反比例函数,求出![]() ,即可知反比例函数解析式,已知点A的纵坐标,代入求得的反比例函数解析式,可求得点A的横坐标,再利用待定系数法,即可求得一次函数解析式;
,即可知反比例函数解析式,已知点A的纵坐标,代入求得的反比例函数解析式,可求得点A的横坐标,再利用待定系数法,即可求得一次函数解析式;
(2)一次函数与y轴交于点C,可求得C的坐标,易证四边形MBOC是平行四边形,OM即为高,四边形![]() 的面积即可求解;
的面积即可求解;
(3)要使反比例函数的值小于一次函数的值,反比例函数图像一定在一次函数图像的下方,观察图像,即可求解自变量的取值范围.
解:(1)∵BM⊥![]() 轴,且BM=OM,
轴,且BM=OM,
∴△BMO为等腰直角三角形,
∵OB=![]() ,
,
∴BM=OM=2,
∴点B的坐标为(-2,-2),
∵点B在双曲线![]() 上,代入
上,代入![]() ,可求得
,可求得![]() ,
,
故反比例函数的解析式为![]() ,
,
∵点A 也是反比例函数上的点,且A点的纵坐标为4,代入![]() ,
,
求得A点坐标为(1,4),
∵点A、B也是直线![]() 上的点,
上的点,
∴ ![]() ,解得
,解得![]() .
.
故一次函数的解析式为![]() .
.
(2)∵ 一次函数![]() 与
与![]() 轴交于点C, 将
轴交于点C, 将![]() 代入解析式,可求得C点的坐标为(0,2)
代入解析式,可求得C点的坐标为(0,2)
∴ BM=OC,又∵BM//OC,
∴四边形MBOC是平行四边形,OM即为平行四边形MBOC的高,
∴四边形MBOC的面积![]() ,
,
故四边形MBOC的面积为4.
(3)根据图像观察可知,要使反比例函数的值小于一次函数的值时,反比例函数图像一定在一次函数图像的下方,包括A(1,4)的右侧,以及B(-2,-2)到![]() 轴这两部分,从而可知,自变量
轴这两部分,从而可知,自变量![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实区中小学“阅读·写字·演讲”三项工程工作,我区各校大力推广阅读活动,某校初二(1)班为了解2月份全班学生课外阅读的情况,调查了全班学生2月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:

根据以上信息解决下列问题:
(1)参加本次问卷调查的学生共有______人,其中2月份读书2册的学生有______人;
(2)补全条形统计图,并求扇形统计图中读书3册所对应扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
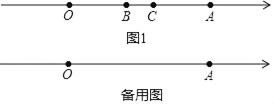
【题目】已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,
(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC﹣OB=![]() AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A.一组对角相等,一组邻角相等的四边形是平行四边形
B.一组对边平行,一组对角相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.一组对边相等,一组对角相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
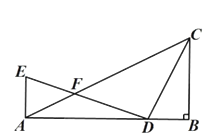
【题目】如图,在△ABC中,∠ABC=90°,D为AB边上一点(BD<BC),AE⊥AB,AE=BD,连接DE交AC于F,若∠AFE=45°,AD=3![]() ,CD=5,则线段AC的长度为_________.
,CD=5,则线段AC的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )

A. ① B. ② C. ①② D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com