
【题目】一次数学课上,小明同学给小刚同学出了一道数形结合的综合题,他是这样出的:如图,数轴上两个动点 M,N 开始时所表示的数分别为﹣10,5,M,N 两点各自以一定的速度在数轴上运动,且 M 点的运动速度为2个单位长度/s.
(1)M,N 两点同时出发相向而行,在原点处相遇,求 N 点的运动速度.
(2)M,N 两点按上面的各自速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?
(3)M,N 两点按上面的各自速度同时出发,向数轴负方向运动,与此同时,C 点从原点出发沿同方向运动,且在运动过程中,始终有 CN:CM=1:2.若干秒后,C 点在﹣12 处,求此时 N 点在数轴上的位置.

【答案】⑴1⑵t=9或t=21⑶-4
【解析】分析:(1)设N点的运动速度为x,M、N两点同时出发相向而行,则他们的时间相等,列出等量关系: ![]() ,解得x即可;
,解得x即可;
(2)此问分两种情况讨论:设经过时间为t后,则N在M的前方,N点经过的路程-M点经过的路程=9;M在N的前方则M点经过的路程-N点经过的路程=6;列出等式解出t即可;
(3)设点C的速度为y,始终有CN∶CM=1∶2,,即:![]() ,得
,得![]() ,当C停留在-12处,所用时间为:
,当C停留在-12处,所用时间为: ![]() 秒,B的位置为5-9=-4.
秒,B的位置为5-9=-4.
本题解析:
(1)设N点的运动速度为x,M、N两点同时出发相向而行,则他们的时间相等,
有: ![]() ,
,
解得![]() ,
,
所以N点的运动速度为1;
(2)设经过时间为t.
则N在M的前方,N点经过的路程-M点经过的路程=6,则
2t-t=15-6,解得t=9.
M在N的前方,M点经过的路程-N点经过的路程=6,则
2t-t=15+6,解得t=21.
(3)设点C的速度为y,始终有CN∶CM=1∶2,
即:![]() ,解得
,解得![]() ,
,
当C停留在-12处,所用时间为: ![]() 秒,
秒,
N的位置为5-9=-4.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】某工程由甲乙两队合做![]() 天完成,厂家需付甲乙两队共
天完成,厂家需付甲乙两队共![]() 元;乙丙两队合做
元;乙丙两队合做![]() 天完成,厂家需付乙丙两队共
天完成,厂家需付乙丙两队共![]() 元;甲丙两队合做
元;甲丙两队合做![]() 天完成全部工程的
天完成全部工程的![]() ,厂家需付甲丙两队共
,厂家需付甲丙两队共![]() 元.
元.
(1)求甲、乙、丙各队单独完成全部工程各需多少天?
(2)若要求不超过![]() 天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB: ![]() 交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.
交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,入射角∠ODE与反射角∠ADC相等,则∠DEB的度数是( )

A. 75°36′ B. 75°12′ C. 74°36′ D. 74°12′
查看答案和解析>>
科目:初中数学 来源: 题型:
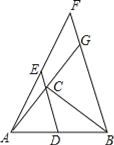
【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=![]() CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,已知Rt△ABC中,AB=BC,AC=2,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),点C在DE上,点B在DF上.
(1)求重叠部分△BCD的面积;
(2)如图2,将直角三角板DEF绕D点按顺时针方向旋转30度,DE交BC于点M,DF交AB于点N.
①求证:DM=DN;
②在此条件下重叠部分的面积会发生变化吗?若发生变化,请求出重叠部分的面积,若不发生变化,请说明理由;
(3)如图3,将直角三角板DEF绕D点按顺时针方向旋转α度(0<α<90),DE交BC于点M,DF交AB于点N,则DM=DN的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com