
【题目】顺次连接平面上![]() 四点得到一个四边形,从①
四点得到一个四边形,从①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 四个条件中任取其中两个,可以得出“四边形
四个条件中任取其中两个,可以得出“四边形![]() 是平行四边形”,这一结论的情况共有( )
是平行四边形”,这一结论的情况共有( )
A.2种B.3种C.4种D.5种
【答案】B
【解析】
根据平行四边形的判定定理可得出答案.
如图,
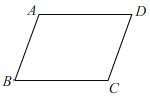
当①AB∥CD,③∠A=∠C时,四边形ABCD为平行四边形;
理由:∵AD∥BC,
∴∠D+∠C=180°,
∵∠A=∠C,
∴∠D+∠A=180°,
∵AB∥CD,
∴四边形ABCD是平行四边形;
当①AB∥CD,④∠B=∠D时,四边形ABCD为平行四边形;理由:同上;
当③∠A=∠C,④∠B=∠D时,四边形ABCD为平行四边形;
理由:在四边形ABCD中,∠A+∠B+∠C+∠D=360°,
∵∠A=∠C,∠B=∠D,
∴2∠A+2∠B=360°
∴∠A+∠B=180°,
∴AD∥BC,
同理:AB∥DC,
∴四边形ABCD是平行四边形;
故选:B.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王师傅承包了一片池塘养水产品,他用总长为88m的围网围成如图所示的5个区域,其中②③④⑤四个区域面积相等.设AH=xm,整个矩形区域的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)当x为何值时,y取最大值?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.

(1)我们先从特殊的倍角三角形入手研究.请你结合图形填空:
三三角形角形 | 角的已知量 |
|
|
图2 | ∠A=2∠B=90° | ||
图3 | ∠A=2∠B=60° |
(2)如图4,对于一般的倍角△ABC,若∠CAB=2∠CBA,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图4给出的辅助线提示加以证明;
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足![]() .
.
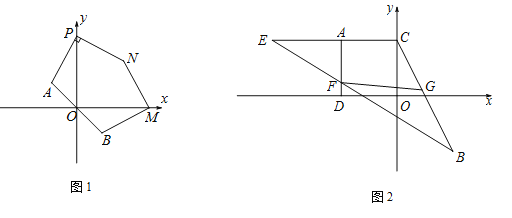
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且![]() ,PA⊥PN,
,PA⊥PN,![]() ,求证:BM⊥MN;
,求证:BM⊥MN;
(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使![]() ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有![]() ,点G是CB上一点,且
,点G是CB上一点,且![]() ,连结FG,求证:
,连结FG,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com