
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )

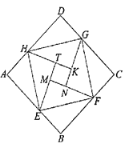
A. ![]() B. 5C. 6D. 9
B. 5C. 6D. 9
科目:初中数学 来源: 题型:
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,
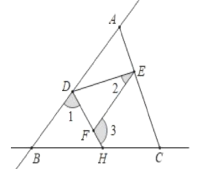
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
已知:PH∥AE,PK∥BC,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.

(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD.
(1)作图,作∠A的平分线AE交CD于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断△AED的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.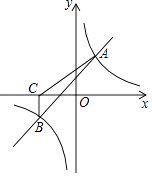
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b< ![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某集团购买了150吨物资打算运往某地支援,现有甲、乙、丙三种车型供选择,每辆汽车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 1000 | 1200 | 1500 |
(1)若全部物资都用甲、乙两种车型来运送,需运费24000元,问分别需甲、乙两种车型各多少辆?
(2)若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送,请你写出可能的运送方案,并帮助该集团找出运费最省的方案(甲、乙、丙三种车辆均要参与运送).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com