
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
已知:PH∥AE,PK∥BC,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
【答案】
(1)解:如图所示,∵OE=80米,OC=ED=100米,AE=60米,BC=70米,
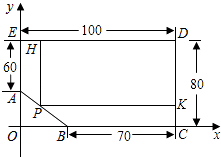
∴OA=20米,OB=30米,
即A、B的坐标为(0,20)、(30,0).
设直线AB的解析式为y=kx+b(k≠0),则 ![]() ,
,
解得, 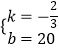 ,
,
则直线AB的解析式为y=﹣ ![]() x+20;
x+20;
(2)解:设点P的坐标为P(x,y).
∵点P在直线AB上,所以点P的坐标可以表示为(x,﹣ ![]() x+20),
x+20),
∴PK=100﹣x,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+ ![]() x,
x,
∴S=(100﹣x)(60+ ![]() x).
x).
【解析】根据题意容易求出A、B的坐标,利用待定系数法可以求出直线AB的解析式;(2)设点P的坐标为P(x,y),则PK=100﹣x,,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+![]() x,,根据矩形的面积公式可以求得函数解析式。
x,,根据矩形的面积公式可以求得函数解析式。
【考点精析】关于本题考查的确定一次函数的表达式和矩形的性质,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图所示,已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
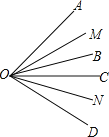
(1)若∠BOC=25°,∠MOB=15°,∠NOD=10°,求∠AOD的大小;
(2)若∠AOD=75°,∠MON=55°,求∠BOC的大小;
(3)若∠AOD=α,∠MON=β,求∠BOC的大小(用含α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(3,4),⊙A的半径为3,延长OA交⊙A于点B,过点B作⊙A的切线,交y轴于点C,则OC长为( )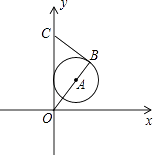
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(8,0),点B的坐标为(6,4),点C的坐标为(0,4),点P从原点O出发,以每秒3的单位长度的速度沿x轴向右运动,点Q从点B出发,以每秒1的单位长度的速度沿线段BC向左运动,P,Q两点同时出发,当点Q运动到点C时,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 时,四边形OPQC为矩形;
(2)当t= 时,线段PQ平分四边形OABC的面积;
(3)在整个运动过程中,当以ACPQ为顶点的四边形为平行四边形时,求该平行四边形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′ 分别为EF、EG、GF的中点,如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
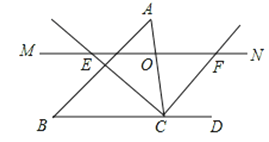
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用960元购进一批服装,并以每件46元的价格全部售完![]() 由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
![]() 该服装店第一次购买了此种服装多少件?
该服装店第一次购买了此种服装多少件?
![]() 两次出售服装共盈利多少元?
两次出售服装共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )

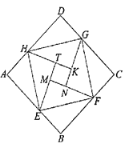
A. ![]() B. 5C. 6D. 9
B. 5C. 6D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com