Question

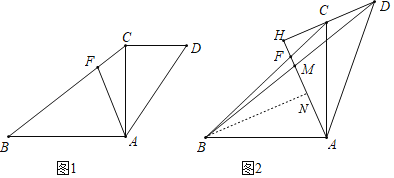
【题目】在△ABC中，∠BAC＝90°，以AC为边向外作△ACD，F为BC上一点，连结AF．

（1）如图1，若∠ACD＝90°，∠CAD＝30°，CD＝1，AB＝BF＝2，求FC的长度．

（2）如图2，若AB＝AC，延长DC交AF延长线于H点，且∠AHD＝90°，∠BCH＝∠CAD，连结BD交AF于M点，求证：CD＝2MH．

Answer 1

【答案】（1）CF＝﹣2；（2）见解析

【解析】

（1）先用30°直角三角形的性质求AD的长，进而可求出AC的长，在△ACB中，BC2＝AB2+AC2，求出BC的长，则CF＝BC﹣BF可求出；

（2）过点B作BN⊥AH，先证明△ABN≌△CAH得AN＝CH，BN＝AH，根据∠BCH＝∠CAD证得△ADH是等腰直角三角形，AH＝DH，再证明△BNM≌△DHM得：HM＝MN，即CD＝2MH．

（1）解：∵∠ACD＝90°，∠CAD＝30°，CD＝1，

∴AD=2，

∴，

在Rt△ABC中，，

∴CF＝BC﹣BF＝﹣2．

（2）证明：过点B作BN⊥AH，

∵∠BAC＝90°，∠ANB＝90°，

∴∠CAH＝∠ABN，

在Rt△ABN和Rt△CAH中，

，

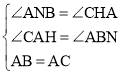∴△ABN≌△CAH（AAS），

∴BN＝AH，AN＝CH，

∵AB＝AC，

∴∠ACB＝45°，

∵∠HCA＝∠CAD+∠ADH，∠HCA＝∠BCH+ACB，∠BCH＝∠CAD，

∴∠ADH＝∠ACB＝45°，

∴AH＝DH，

∴BN＝DH，

在Rt△BNM和Rt△DHM中，

，

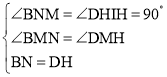∴△BNM≌△DHM（AAS），

∴MH＝MN，

∵AH＝AN+HN，DH＝CH+CD，

∴HN＝CD，

∴CD＝2MH．