
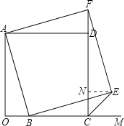
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 上任意一点,以
上任意一点,以![]() 为边作正方形
为边作正方形![]() .
.
①连接![]() ,求证:
,求证:![]() ;
;
②连接![]() ,猜想
,猜想![]() 的度数,并证明你的结论;
的度数,并证明你的结论;
③设点![]() 在线段
在线段![]() 上运动,
上运动,![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,试求
,试求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.

【答案】(1)证明见解析;(2)![]() 的度数为
的度数为![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)根据三角形全等的判定定理,可以证得△AOB≌△ADF,进而得出结论.
(2)过E作CD的垂线,得出所构成的三角形为等边三角形,继而得出所求角的度数为45°.
(3)由正方形AOCD的面积,可以而出边长,又有OB的长,根据勾股定理,得出正方形ABEF的边长,继而求出面积,在边OC上运动,则可得出x的取值范围.
![]() 证明:∵正方形
证明:∵正方形![]() ,
,
∴![]() ,
,![]() ,
,
∵正方形![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 猜想
猜想![]() 的度数为
的度数为![]()
证明:如图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
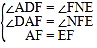 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴三角形![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() .
.
![]() 解:∵
解:∵![]() ,
,
∴![]() ,
,
∵正方形![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在线段
在线段![]() 上运动,
上运动,
∴![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A、B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥,A、B两个果园分别需要110吨和70吨有机化肥.甲仓库到A、B两个果园的路程分别为15千米和25千米,乙仓库到A、B两个果园的路程都是20千米.设甲仓库运往A果园x吨有机化肥,解答下列问题:
(1)甲仓库运往B果园 吨有机化肥,乙仓库运往B果园 吨有机化肥;
(2)若汽车每吨每千米的运费为2元,设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?此时的总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,以AC为边向外作△ACD,F为BC上一点,连结AF.
(1)如图1,若∠ACD=90°,∠CAD=30°,CD=1,AB=BF=2,求FC的长度.
(2)如图2,若AB=AC,延长DC交AF延长线于H点,且∠AHD=90°,∠BCH=∠CAD,连结BD交AF于M点,求证:CD=2MH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10……) 和“正方形数”(如1,4,9,16……),在小于200的数中,设最大的“三角形数”为t,最大的“正方形数”为m,则t+m的值为( )

A.33B.301C.386D.571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com