Question

【题目】探究：如图①，在四边形中，，，于点．若，求四边形的面积．

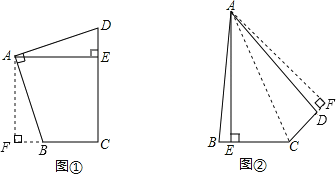
应用：如图②，在四边形中，，，于点．若，，，则四边形的面积为________．

Answer 1

【答案】

【解析】

探究：过点A作AF⊥CB，交CB的延长线于点F，先判定四边形AFCE为矩形，根据矩形的四个角都是直角可得∠FAE=90°，然后利用同角的余角相等求出∠FAB=∠EAD，再利用“角角边”证明△AFB和△AED全等，根据全等三角形对应边相等可得AE=AF，从而得到四边形AFCE是正方形，然后根据正方形的面积公式列计算即可得解；

应用：过点A作AF⊥CD交CD的延长线于F，连接AC，根据同角的补角相等可得∠ABC=∠ADF，然后利用“角角边”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AF=AE，再根据S四边形ABCD=S△ABC+S△ACD列式计算即可得解．

解：探究：如图①，过点A作AF⊥CB，交CB的延长线于点F，

∵AE⊥CD，∠BCD=90°，

∴四边形AFCE为矩形，

∴∠FAE=90°，

∴∠FAB+∠BAE=90°，

∵∠EAD+∠BAE=90°，

∴∠FAB=∠EAD，

∵在△AFB和△AED中，

，

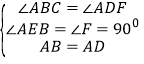∴△AFB≌△AED（AAS），

∴AF=AE，

∴四边形AFCE为正方形，

∴S四边形ABCD=S正方形AFCE=AE2=102=100；

应用：如图，过点A作AF⊥CD交CD的延长线于F，连接AC，

则∠ADF+∠ADC=180°，

∵∠ABC+∠ADC=180°，

∴∠ABC=∠ADF，

∵在△ABE和△ADF中，

,

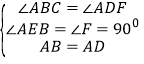∴△ABE≌△ADF（AAS），

∴AF=AE=19，

∴S四边形ABCD=S△ABC+S△ACD

=BCAE+CDAF

=×10×19+×6×19

=95+57

=152．

故答案为：152．