
ЁОЬтФПЁПЮЊСЫБЃЛЄЛЗОГКЭЬсИпЙћЪїВњСПЃЌФГЙћХЉМЦЛЎДгМзЁЂввСНИіВжПтгУЦћГЕЯђAЁЂBСНИіЙћдАдЫЫЭгаЛњЛЏЗЪЃЌМзЁЂввСНИіВжПтЗжБ№ПЩдЫГі80ЖжКЭ100ЖжгаЛњЛЏЗЪЃЌAЁЂBСНИіЙћдАЗжБ№ашвЊ110ЖжКЭ70ЖжгаЛњЛЏЗЪЃЎМзВжПтЕНAЁЂBСНИіЙћдАЕФТЗГЬЗжБ№ЮЊ15ЧЇУзКЭ25ЧЇУзЃЌввВжПтЕНAЁЂBСНИіЙћдАЕФТЗГЬЖМЪЧ20ЧЇУзЃЎЩшМзВжПтдЫЭљAЙћдАxЖжгаЛњЛЏЗЪЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзВжПтдЫЭљBЙћдАЁЁ ЁЁЖжгаЛњЛЏЗЪЃЌввВжПтдЫЭљBЙћдАЁЁ ЁЁЖжгаЛњЛЏЗЪЃЛ
ЃЈ2ЃЉШєЦћГЕУПЖжУПЧЇУзЕФдЫЗбЮЊ2дЊЃЌЩшзмдЫЗбЮЊyдЊЃЌЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЌВЂЧѓЕБМзВжПтдЫЭљAЙћдАЖрЩйЖжгаЛњЛЏЗЪЪБЃЌзмдЫЗбзюЪЁЃПДЫЪБЕФзмдЫЗбЪЧЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉЃЈ80ЉxЃЉЃЌЃЈxЉ10ЃЉЃЛЃЈ2ЃЉyЙигкxЕФКЏЪ§БэДяЪНЪЧyЃНЉ20x+8000ЃЌЕБМзВжПтдЫЭљAЙћдА80ЖжгаЛњЛЏЗЪЪБЃЌзмдЫЗбзюЪЁЃЌДЫЪБЕФзмдЫЗб6400дЊ
ЁОНтЮіЁП
МзВжПтдЫЭљAЙћдАxЖжгаЛњЛЏЗЪЃЌдђЪЃЯТ(80-x)ЖжгІШЋВПдЫЭљBЙћдА,вђAЙћдАЙВашЛЏЗЪ110ЖжЃЌВю(110-x)ЖжжЛФмДгввВжПтдЫШЅСЫЃЌЫљвдввВжПташдЫЭљAЙћдАЃЈ110-xЃЉЖжЃЌвђBЙћдАашвЊ70ЖжЃЌЫљвдЛЙВю70-ЃЈ80-xЃЉ=(x-10)ЖжжЛФмДгввВжПтдЫЭљЃЌЫљвдввВжПтдЫЭљBЙћдА(x-10)ЖжгаЛњЛЏЗЪЃЛЃЈ2ЃЉИљОнзмдЫЗб=МзВжПтдЫЭљAЙћдАЕФдЫЗб+МзВжПтдЫЭљBЙћдАЕФдЫЗб+ввВжПтдЫЭљAЙћдАЕФдЫЗб+ввВжПтдЫЭљBЙћдАЕФдЫЗбЃЌМДПЩЕУГіКЏЪ§ЙиЯЕЪНЃЌИљОнЫљЕУКЏЪ§аджЪЃЌМАздБфСПШЁжЕЗЖЮЇЃЌМДПЩзїГіД№АИ.
ЃЈ1ЃЉМзВжПтдЫЭљAЙћдАxЖжгаЛњЛЏЗЪЃЌдђМзВжПтдЫЭљBЙћдАЃЈ80ЉxЃЉЖжгаЛњЛЏЗЪЃЌввВжПтдЫЭљAЙћдАЃЈ110ЉxЃЉЖжгаЛњЛЏЗЪЃЌввВжПтдЫЭљBЙћдА70ЉЃЈ80ЉxЃЉЃНЃЈxЉ10ЃЉЖжгаЛњЛЏЗЪ.
ЙЪД№АИЮЊЃКЃЈ80ЉxЃЉЃЌЃЈxЉ10ЃЉЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЕУЃЌ
yЃН15ЁС2x+25ЁС2ЃЈ80ЉxЃЉ+20ЁС2ЃЈ110ЉxЃЉ+20ЁС2ЃЈxЉ10ЃЉЃНЉ20x+8000ЃЌ
Ёп![]()
Ёр10ЁмxЁм80ЃЌ
ЁпyгыxжЎМфЪЧвЛДЮКЏЪ§ЙиЯЕЃЌЧвk=-20<0
ЁрyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБxЃН80ЪБЃЌyШЁЕУзюаЁжЕЃЌДЫЪБyЃН-20ЁС80+8000=6400дЊЃЌ
Д№ЃКyЙигкxЕФКЏЪ§БэДяЪНЪЧyЃНЉ20x+8000ЃЌЕБМзВжПтдЫЭљAЙћдА80ЖжгаЛњЛЏЗЪЪБЃЌзмдЫЗбзюЪЁЃЌДЫЪБЕФзмдЫЗб6400дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
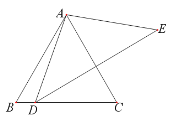
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDдкBCЩЯЃЌЁїADEЪЧЕШбќШ§НЧаЮЃЌAD ЃНAE ЃЌЁЯDAE ЃН100ЁуЃЌЕБDEЁЭACЪБЃЌЧѓЁЯBADКЭЁЯEDCЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ![]() ЕФе§ЗНаЮ
ЕФе§ЗНаЮ![]() ЕФЖдНЧЯпНЛгкЕу
ЕФЖдНЧЯпНЛгкЕу![]() ЃЌАбБп
ЃЌАбБп![]() ЁЂ
ЁЂ![]() ЗжБ№ШЦЕу
ЗжБ№ШЦЕу![]() ЁЂ
ЁЂ![]() ЭЌЪБФцЪБеыа§зЊ
ЭЌЪБФцЪБеыа§зЊ![]() ЕУЫФБпаЮ
ЕУЫФБпаЮ![]() ЃЌЦфЖдНЧЯпНЛЕуЮЊ
ЃЌЦфЖдНЧЯпНЛЕуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЯТСаНсТлЃК
ЃЎЯТСаНсТлЃК
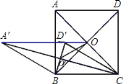
ЂйЫФБпаЮ![]() ЮЊСтаЮЃЛ
ЮЊСтаЮЃЛ
Ђк![]() ЃЛ
ЃЛ
ЂлЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЛ
ЃЛ
ЂмЕу![]() дЫЖЏЕНЕу
дЫЖЏЕНЕу![]() ЕФТЗОЖЪЧЯпЖЮ
ЕФТЗОЖЪЧЯпЖЮ![]() ЃЎЦфжае§ШЗЕФНсТлЙВгаЃЈ ЃЉ
ЃЎЦфжае§ШЗЕФНсТлЙВгаЃЈ ЃЉ
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКе§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ

![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧе§ЗНаЮТ№ЃПЮЊЪВУДЃП
ЪЧе§ЗНаЮТ№ЃПЮЊЪВУДЃП
![]() Шєе§ЗНаЮ
Шєе§ЗНаЮ![]() ЕФБпГЄЮЊ
ЕФБпГЄЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧыЧѓГіЫФБпаЮ
ЃЌЧыЧѓГіЫФБпаЮ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCDЦНЗжЁЯACBЃЌЕуDЪЧABЕФжаЕуЃЌAEЁЮDCЃЌAEНЛBCЕФбгГЄЯпгкЕуEЃЌЧвЁЯACE=60ЁуЃЌBC=8.ЧѓЁїACEЕФжмГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЖЏЕуЃЌЕу
ЩЯвЛЖЏЕуЃЌЕу![]() вд
вд![]() ЕФЫйЖШДгЕу
ЕФЫйЖШДгЕу![]() ГіЗЂби
ГіЗЂби![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЎЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЎЩшдЫЖЏЪБМфЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ________
________![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊЕШбќШ§НЧаЮЃЎ
ЮЊЕШбќШ§НЧаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ЯШЛЏМђЃЌдйЧѓжЕЃК(aЃb)2ЃЋb(3aЃb)Ѓa2ЃЌЦфжаaЃН2ЃЌbЃН6ЃЛ
(2) вбжЊ2a2ЃЋ3aЃ6ЃН0ЃЌЧѓДњЪ§ЪН3a(2aЃЋ1)Ѓ(2aЃЋ1)(2aЃ1)ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЪЧ
ЪЧ![]() ЩЯШЮвтвЛЕуЃЌвд
ЩЯШЮвтвЛЕуЃЌвд![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЎ
ЃЎ
ЂйСЌНг![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкСЌНг![]() ЃЌВТЯы
ЃЌВТЯы![]() ЕФЖШЪ§ЃЌВЂжЄУїФуЕФНсТлЃЛ
ЕФЖШЪ§ЃЌВЂжЄУїФуЕФНсТлЃЛ
ЂлЩшЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЃЌ
ЩЯдЫЖЏЃЌ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГі
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮ![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() жаЕуЁЂ
жаЕуЁЂ![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ![]() ЮЊ
ЮЊ![]() бгГЄЯпЩЯвЛЕуЃЌСЌНг
бгГЄЯпЩЯвЛЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гыЕу
гыЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com