
【题目】矩形![]() 中,
中,![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() 并延长交
并延长交![]() 与点
与点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.

【答案】证明见解析.
【解析】
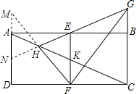
设AC、EF相交于点K,延长FH与DA的延长线相交于点M,延长GH与AD相交于点N,求出△AMH和△KFH相似,根据相似三角形对应边成比例可得![]() =
=![]() ,求出△ANH和△KEH相似,根据相似三角形对应边成比例可得
,求出△ANH和△KEH相似,根据相似三角形对应边成比例可得![]() =
=![]() ,然后求出AM=AN,再利用“角边角”证明△AEN和△BEG全等,根据全等三角形对应边相等可得AN=BG,然后求出DM=CG,再利用“边角边”证明△DFM和△CFG全等,根据全等三角形对应角相等可得∠M=∠CGF,然后根据平行线的性质可得∠HFE=∠M,∠EFG=∠CGF,再等量代换即可得证.
,然后求出AM=AN,再利用“角边角”证明△AEN和△BEG全等,根据全等三角形对应边相等可得AN=BG,然后求出DM=CG,再利用“边角边”证明△DFM和△CFG全等,根据全等三角形对应角相等可得∠M=∠CGF,然后根据平行线的性质可得∠HFE=∠M,∠EFG=∠CGF,再等量代换即可得证.
证明:如图,设![]() 、
、![]() 相交于点
相交于点![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,延长
,延长![]() 与
与![]() 相交于点
相交于点![]() ,
,
∵![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,![]() 是对角线,
是对角线,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
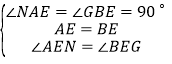 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
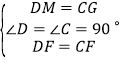 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A、B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥,A、B两个果园分别需要110吨和70吨有机化肥.甲仓库到A、B两个果园的路程分别为15千米和25千米,乙仓库到A、B两个果园的路程都是20千米.设甲仓库运往A果园x吨有机化肥,解答下列问题:
(1)甲仓库运往B果园 吨有机化肥,乙仓库运往B果园 吨有机化肥;
(2)若汽车每吨每千米的运费为2元,设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?此时的总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10……) 和“正方形数”(如1,4,9,16……),在小于200的数中,设最大的“三角形数”为t,最大的“正方形数”为m,则t+m的值为( )

A.33B.301C.386D.571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
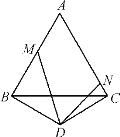
【题目】如图,已知等边三角形△ABC边长为a,等腰三角形△BDC中,∠BDC=120,∠MDN=60,角的两边分别交AB,AC于点M,N,连结MN.则△AMN的周长为( )
A.aB.2aC.3aD.4a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一刻度尺检验一个四边形是否为矩形,以下方法可行的有________.(只要填序号即可)
①量出四边及两条对角线,比较对边是否相等,对角线是否相等.
②量出对角线的交点到四个顶点的距离,看是否相等.
③量出一组邻边的长![]() 、
、![]() 以及和这两边组成三角形的那条对角线的长
以及和这两边组成三角形的那条对角线的长![]() ,计算是否有
,计算是否有![]() .
.
④量出两条对角线长,看是否相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() ,抛物线
,抛物线![]() .
.
![]() 当
当![]() ,
,![]() 时,求直线
时,求直线![]() 与抛物线
与抛物线![]() 的交点坐标;
的交点坐标;
![]() 当
当![]() ,
,![]() 时,将直线
时,将直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线
后与抛物线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),求
点的左侧),求![]() ,
,![]() 两点的坐标;
两点的坐标;
![]() 若将
若将![]() 中的条件“
中的条件“![]() ”去掉,其他条件不变,且
”去掉,其他条件不变,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com