Question

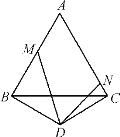
【题目】如图，已知等边三角形△ABC边长为a，等腰三角形△BDC中，∠BDC＝120，∠MDN＝60，角的两边分别交AB，AC于点M，N，连结MN．则△AMN的周长为( )

A.aB.2aC.3aD.4a

Answer 1

【答案】B

【解析】

根据题目已知条件无法求出三条边的长，只能把三条边长用其它已知边长来表示，所以需要作辅助线，延长AB至F，使BF=CN，连接DF，通过证明△BDF≌△CDN及△DMN≌△DMF，从而得出MN=MF，△AMN的周长等于AB+AC的长．

解：∵△BDC是等腰三角形，且∠BDC=120°
∴∠BCD=∠DBC=30°
∵△ABC是边长为3的等边三角形
∴∠ABC=∠BAC=∠BCA=60°
∴∠DBA=∠DCA=90°
延长AB至F，使BF=CN，连接DF，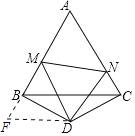

在Rt△BDF和Rt△CND中，BF=CN，DB=DC
∴Rt△BDF≌Rt△CDN（HL），
∴∠BDF=∠CDN，DF=DN
∵∠MDN=60°
∴∠BDM+∠CDN=60°
∴∠BDM+∠BDF=60°，∠FDM=60°=∠MDN，DM为公共边
∴△DMN≌△DMF（SAS），
∴MN=MF
∴△AMN的周长是：AM+AN+MN=AM+MB+BF+AN=AB+AC=2a，
故选：B．