
ЁОЬтФПЁПвдЯТЫЕЗЈКЯРэЕФЪЧЃЈ ЃЉ
A. ФГВЪЦБжаНБЕФЛњЛсЪЧ![]() ЃЌФЧУДФГШЫТђСЫ
ЃЌФЧУДФГШЫТђСЫ![]() еХВЪЦБЃЌПЯЖЈгавЛеХжаНБ
еХВЪЦБЃЌПЯЖЈгавЛеХжаНБ
B. аЁУРдк![]() ДЮХзЭМЖЄЕФЪдбщжаЗЂЯжСЫ
ДЮХзЭМЖЄЕФЪдбщжаЗЂЯжСЫ![]() ДЮЖЄМтГЏЩЯЃЌОнДЫЫћШЯЮЊЖЄМтГЏЩЯЕФИХТЪЮЊ
ДЮЖЄМтГЏЩЯЃЌОнДЫЫћШЯЮЊЖЄМтГЏЩЯЕФИХТЪЮЊ![]()
C. ХзжРвЛУЖжЪЕиОљдШЕФгВБвЃЌГіЯжЁАе§УцЁБКЭЁАЗДУцЁБЕФИХТЪЯрЕШЃЌвђДЫХз![]() ДЮЕФЛАЃЌвЛЖЈга
ДЮЕФЛАЃЌвЛЖЈга![]() ДЮЁАе§УцЁБЃЌ
ДЮЁАе§УцЁБЃЌ![]() ДЮЁАЗДУцЁБ
ДЮЁАЗДУцЁБ
D. дквЛДЮПЮЬУЩЯНјааЕФЪдбщжаЃЌМзЁЂввСНзщЭЌбЇЙРМЦвЛУЖгВБвТфЕиКѓе§УцГЏЩЯЕФИХТЪЮЊ![]() КЭ
КЭ![]()
ЁОД№АИЁПD
ЁОНтЮіЁП
ДѓСПЗДИДЪдбщЪБЃЌФГЪТМўЗЂЩњЕФЦЕТЪЛсЮШЖЈдкФГИіГЃЪ§ЕФИННќЃЌетИіГЃЪ§ОЭНазіЪТМўИХТЪЕФЙРМЦжЕЃЌЖјВЛЪЧвЛжжБиШЛЕФНсЙћЃЌОнДЫМДПЩХаЖЯЃЎ
AЁЂФГВЪЦБжаНБЕФЛњЛсЪЧ![]() ЃЌФЧУДФГШЫТђСЫ24еХВЪЦБЃЌВЛвЛЖЈжаНБЃЌДЫбЁЯюДэЮѓЃЛ
ЃЌФЧУДФГШЫТђСЫ24еХВЪЦБЃЌВЛвЛЖЈжаНБЃЌДЫбЁЯюДэЮѓЃЛ
BЁЂЪдбщДЮЪ§ЬЋЩйЃЌВЛФмЫЕУїИХТЪвЛЖЈЪЧ30%ЃЌДЫбЁЯюДэЮѓЃЛ
CЁЂХзжРвЛУЖжЪЕиОљдШЕФгВБвЃЌГіЯжЁАе§УцЁБКЭЁАЗДУцЁБЕФИХТЪЯрЕШЃЌвђДЫХз1000ДЮЕФЛАЃЌДѓдМга500ДЮЁАе§УцЁБЃЌ500ДЮЁАЗДУцЁБЃЌДЫбЁЯюДэЮѓЃЛ
DЁЂдквЛДЮПЮЬУЩЯНјааЕФЪдбщжаЃЌМзЁЂввСНзщЭЌбЇЙРМЦвЛУЖгВБвТфЕиКѓе§УцГЏЩЯЕФИХТЪЮЊ0.48КЭ0.51ЃЌДЫбЁЯюе§ШЗЃЛ
ЙЪбЁЃКDЃЎ


 аТЬтаЭШЋГЬМьВтЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТЬтаЭШЋГЬМьВтЦкФЉГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШБпШ§НЧаЮЁїABCБпГЄЮЊaЃЌЕШбќШ§НЧаЮЁїBDCжаЃЌЁЯBDCЃН120ЃЌЁЯMDNЃН60ЃЌНЧЕФСНБпЗжБ№НЛABЃЌACгкЕуMЃЌNЃЌСЌНсMNЃЎдђЁїAMNЕФжмГЄЮЊ( )
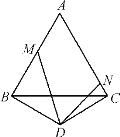
A.aB.2aC.3aD.4a
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцЕФВФСЯЃЌЛиД№ЮЪЬтЃК
АЎЖЏФдНюЕФаЁУїЗЂЯжЖўДЮШ§ЯюЪНвВПЩвдХфЗНЃЌДгЖјНтОівЛаЉЮЪЬтЃЎ
Р§ШчЃКx2Љ6x+10=ЃЈx2Љ6x+9ЃЉ+1=ЃЈxЉ3ЃЉ2+1Ён0ЃЛвђДЫx2Љ6x+10газюаЁжЕЪЧ1ЃЎ
ЃЈ1ЃЉГЂЪдЃКЉ3x2Љ6x+5=Љ3ЃЈx2+2x+1Љ1ЃЉ+5=Љ3ЃЈx+1ЃЉ2+8ЃЌвђДЫЉ3x2Љ6x+5газюДѓжЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉгІгУЃКгаГЄЮЊ28УзЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНЕФзюДѓПЩгУГЄЖШЮЊ16УзЃЉЃЌЮЇГЩвЛИіГЄЗНаЮЕФЛЈЦдЃЎФмЮЇГЩУцЛ§зюДѓЕФЛЈЦдТ№ЃПШчЙћФмЃЌЧыЧѓГізюДѓУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРђЕФАжАжТђСЫНёФъЦпдТЗнШЅЩЯКЃПДЪРВЉЛсЕФвЛеХУХЦБЃЌЫ§КЭИчИчСНШЫЖМКмЯыШЅЙлПДЃЌПЩУХЦБжЛгавЛеХЃЌЖСОХФъМЖЕФИчИчЯыСЫвЛИіАьЗЈЃЌФУСЫАЫеХЦЫПЫХЦЃЌНЋЪ§зжЮЊ1ЃЌ2ЃЌ3ЃЌ5ЕФЫФеХХЦИјаЁРђЃЌНЋЪ§зжЮЊ4ЃЌ6ЃЌ7ЃЌ8ЕФЫФеХХЦСєИјздМКЃЌВЂАДШчЯТгЮЯЗЙцдђНјааЃКаЁРђКЭИчИчДгИїздЕФЫФеХХЦжаЫцЛњГщГівЛеХЃЌШЛКѓНЋГщГіЕФСНеХЦЫПЫХЦЪ§зжЯрМгЃЌШчЙћКЭЮЊХМЪ§ЃЌдђаЁРђШЅЃЛШчЙћКЭЮЊЦцЪ§ЃЌдђИчИчШЅЃЎ
ЃЈ1ЃЉЧыгУЪ§зДЭМЛђСаБэЕФЗНЗЈЧѓаЁРђШЅЩЯКЃПДЪРВЉЛсЕФИХТЪЃЛ
ЃЈ2ЃЉИчИчЩшМЦЕФгЮЯЗЙцдђЙЋЦНТ№ЃПШєЙЋЦНЃЌЧыЫЕУїРэгЩЃЛШєВЛЙЋЦНЃЌЧыФуЩшМЦвЛжжЙЋЦНЕФгЮЯЗЙцдђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮ.

ЃЈ1ЃЉзїЭМЃЌзїЁЯAЕФЦНЗжЯпAEЃЌНЛCDгкЕуE.(гУГпЙцзїЭМЗЈ,БЃСєзїЭМКлМЃ,ВЛвЊЧѓаДзїЗЈ);
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌХаЖЯADгыDEЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ЃЎ
ЃЎ
![]() ЕБ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓжБЯп
ЪБЃЌЧѓжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЕФНЛЕузјБъЃЛ
ЕФНЛЕузјБъЃЛ
![]() ЕБ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌНЋжБЯп
ЪБЃЌНЋжБЯп![]() ШЦдЕуФцЪБеыа§зЊ
ШЦдЕуФцЪБеыа§зЊ![]() КѓгыХзЮяЯп
КѓгыХзЮяЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈ
СНЕуЃЈ![]() Еудк
Еудк![]() ЕуЕФзѓВрЃЉЃЌЧѓ
ЕуЕФзѓВрЃЉЃЌЧѓ![]() ЃЌ
ЃЌ![]() СНЕуЕФзјБъЃЛ
СНЕуЕФзјБъЃЛ
![]() ШєНЋ
ШєНЋ![]() жаЕФЬѕМўЁА
жаЕФЬѕМўЁА![]() ЁБШЅЕєЃЌЦфЫћЬѕМўВЛБфЃЌЧв
ЁБШЅЕєЃЌЦфЫћЬѕМўВЛБфЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЛюЖЏПЮЩЯЃЌаЁЋhЯывЊРћгУЫљбЇЕФЪ§бЇжЊЪЖВтСПФГИіНЈжўЕиЫљдкЩНЦТAEЕФИпЖШЃЌЫ§ЯШдкЩННХЯТЕФЕуEДІВтЕУЩНЖЅAЕФбіНЧЪЧ30ЁуЃЌШЛКѓЃЌЫ§бизХЦТЖШi=1ЃК1ЕФаБЦТАДЫйЖШ20Уз/ЗжВНаа15ЗжжгЕНДяCДІЃЌДЫЪБЃЌВтЕУЕуAЕФИЉНЧЪЧ15ЁуЃЎЭМжаЕуAЁЂBЁЂEЁЂDЁЂCдкЭЌвЛЦНУцФкЃЌЧвЕуDЁЂEЁЂBдкЭЌвЛЫЎЦНжБЯпЩЯЃЌЧѓГіНЈжўЕиЫљдкЩНЦТAEЕФИпЖШABЃЎЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃК![]() Ёж1.41ЃЉЃЎ
Ёж1.41ЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§ЕФЭМЯѓЙ§Еу![]() ЃЎ
ЃЎ
![]() ЧѓКЏЪ§ЕФНтЮіЪНЃЎ
ЧѓКЏЪ§ЕФНтЮіЪНЃЎ![]() Ыц
Ыц![]() ЕФдіДѓЖјШчКЮБфЛЏЃП
ЕФдіДѓЖјШчКЮБфЛЏЃП
![]() Еу
Еу![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ФФаЉЕудкЭМЯѓЩЯЃП
ФФаЉЕудкЭМЯѓЩЯЃП
![]() ЛГіетИіКЏЪ§ЕФЭМЯѓЃЎ
ЛГіетИіКЏЪ§ЕФЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ4ЃЌвбжЊХзЮяЯпy=ax2+bx+cЃЈaЃО0ЃЉОЙ§ЕуAЃЈ2ЃЌ0ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЌНЛyжсгкЕуCЃЌЧвSЁїABC=16ЃЎ
ЃЈ1ЃЉЧѓЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЦфЖдГЦжсЃЛ
ЃЈ3ЃЉШєе§ЗНаЮDEFGФкНггкХзЮяЯпКЭxжсЃЈБпFGдкxжсЩЯЃЌЕуDЃЌEЗжБ№дкХзЮяЯпЩЯЃЉЃЌЧѓSе§ЗНаЮDEFGЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com