
【题目】已知直线![]() ,抛物线
,抛物线![]() .
.
![]() 当
当![]() ,
,![]() 时,求直线
时,求直线![]() 与抛物线
与抛物线![]() 的交点坐标;
的交点坐标;
![]() 当
当![]() ,
,![]() 时,将直线
时,将直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线
后与抛物线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),求
点的左侧),求![]() ,
,![]() 两点的坐标;
两点的坐标;
![]() 若将
若将![]() 中的条件“
中的条件“![]() ”去掉,其他条件不变,且
”去掉,其他条件不变,且![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】有六张分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为![]() ,将该卡片上的数字加
,将该卡片上的数字加![]() 记为
记为![]() ,则函数
,则函数![]() 的图象不过点
的图象不过点![]() 且方程
且方程![]() 有实数解的概率为________.
有实数解的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 某彩票中奖的机会是![]() ,那么某人买了
,那么某人买了![]() 张彩票,肯定有一张中奖
张彩票,肯定有一张中奖
B. 小美在![]() 次抛图钉的试验中发现了
次抛图钉的试验中发现了![]() 次钉尖朝上,据此他认为钉尖朝上的概率为
次钉尖朝上,据此他认为钉尖朝上的概率为![]()
C. 抛掷一枚质地均匀的硬币,出现“正面”和“反面”的概率相等,因此抛![]() 次的话,一定有
次的话,一定有![]() 次“正面”,
次“正面”,![]() 次“反面”
次“反面”
D. 在一次课堂上进行的试验中,甲、乙两组同学估计一枚硬币落地后正面朝上的概率为![]() 和
和![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,荧光屏上的甲、乙两个光斑(可看作点)分别从相距8cm的A,B两点同时开始沿线段AB运动,运动工程中甲光斑与点A的距离S1(cm)与时间t(s)的函数关系图象如图2,乙光斑与点B的距离S2(cm)与时间t(s)的函数关系图象如图3,已知甲光斑全程的平均速度为1.5cm/s,且两图象中△P1O1Q1≌P2Q2O2,下列叙述正确的是( )

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系![]() 中,对于点
中,对于点![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称点
,则称点![]() 为点
为点![]() 的变限点。例如:点
的变限点。例如:点![]() 的变限点的坐标
的变限点的坐标![]() ,点
,点![]() 的变限点的坐标
的变限点的坐标![]() 。
。
(1)点![]() 的变限点的坐标是 ;点
的变限点的坐标是 ;点![]() 的变限点的坐标是 .
的变限点的坐标是 .
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在直线
在直线![]() 上,其变限点为
上,其变限点为![]() ,若
,若![]() (
(![]() 为坐标原点)的面积等于
为坐标原点)的面积等于![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)已知点![]() 在函数
在函数![]() 的图象上,其变限点
的图象上,其变限点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
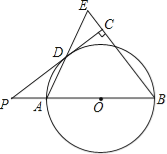
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com