
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
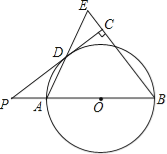
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】(1)见解析;(2)3
【解析】
试题(1)连接OD,由PD切⊙O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结果;
(2)由(1)知,OD∥BE,得到∠POD=∠B,根据三角函数的定义即可得到结果.
试题解析:(1)证明:连接OD,
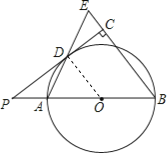
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴∠ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:由(1)知,OD∥BE,
∴∠POD=∠B,
∴cos∠POD=cosB=![]() ,
,
在Rt△POD中,cos∠POD=![]() ,
,
∵OD=OA,PO=PA+OA=2+OA,
∴![]() ,
,
∴OA=3,
∴⊙O半径=3.


科目:初中数学 来源: 题型:
【题目】已知直线![]() ,抛物线
,抛物线![]() .
.
![]() 当
当![]() ,
,![]() 时,求直线
时,求直线![]() 与抛物线
与抛物线![]() 的交点坐标;
的交点坐标;
![]() 当
当![]() ,
,![]() 时,将直线
时,将直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线
后与抛物线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),求
点的左侧),求![]() ,
,![]() 两点的坐标;
两点的坐标;
![]() 若将
若将![]() 中的条件“
中的条件“![]() ”去掉,其他条件不变,且
”去掉,其他条件不变,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加理化实验操作测试,学校进行了6次模测试,成绩如表所示:(单位:分)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
乙 | 7 | 8 | 9 | 10 | 10 | 10 | a | b |
(1)根据图表信息,求表格中a,b的值;
(2)已知甲的成绩的方差等于1,请计算乙的成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:像(![]() +
+![]() )(
)(![]()
![]() )=3,
)=3,![]()
![]() =a(a≥0),(
=a(a≥0),(![]() +1)(
+1)(![]() ﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:
﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:![]() 与
与![]() ,
,![]() +1与
+1与![]() ﹣1,2
﹣1,2![]() +3
+3![]() 与2
与2![]() ﹣3
﹣3![]() 等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如:![]() ;
; ;
;
解答下列问题:
(1)3﹣![]() 与 互为有理化因式,将
与 互为有理化因式,将![]() 分母有理化得 .
分母有理化得 .
(2)计算:2﹣![]() ;
;
(3)观察下面的变形规律并解决问题.
①![]() =
=![]() ﹣1,
﹣1,![]() =
=![]()
![]() ,
,![]() =
=![]() ,…,若n为正整数,请你猜想:
,…,若n为正整数,请你猜想:![]() = .
= .
②计算:(![]() +
+![]() +
+![]() +…+
+…+![]() )×(
)×(![]() +1).
+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4,已知抛物线y=ax2+bx+c(a>0)经过点A(2,0),B(6,0),交y轴于点C,且S△ABC=16.
(1)求点C的坐标;
(2)求抛物线的解析式及其对称轴;
(3)若正方形DEFG内接于抛物线和x轴(边FG在x轴上,点D,E分别在抛物线上),求S正方形DEFG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
在⊙I中,弦AF与DE相交于点Q,则AQQF=DQQE.你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,等边△ABC的边BC在x轴上,高AO在y轴的正半轴上,点Q(0,1)是等边△ABC的重心,过点Q的直线分别交边AB、AC于点D、E,直线DE绕点Q转动,设∠OQD=α(60°<α<120°),△ADE的外接圆⊙I交y轴正半轴于点F,连接EF.
(1)填空:AB= ;
(2)在直线DE绕点Q转动的过程中,猜想:![]() 与
与![]() 的值是否相等?试说明理由.
的值是否相等?试说明理由.
(3)①求证:AQ2=ADAE﹣DQQE;
②记AD=a,AE=b,DQ=m,QE=m(a、b、m、n均为正数),请直接写出mn的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点, 连结BM、MN,则BM+MN的最小值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣4,0),点C是y轴正半轴上的一点,且∠ACB=90°,AC=BC

(1)如图①,若点B在第四象限,C(0,2),求点B的坐标;
(2)如图②,若点B在第二象限,以OC为直角边在第一象限作等腰Rt△COF,连接BF,交y轴于点M,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).

(1)A点所表示的实际意义是 ;![]() = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度
的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com