
【题目】如图所示,点![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;②
;②![]() 一定是等腰三角形;③
一定是等腰三角形;③![]() ;④
;④![]() ,
,
其中正确结论的序号是________.

【答案】①③④
【解析】
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,对边相等可得PF=EC,再判断出△PDF是等腰直角三角形,然后根据等腰直角三角形的斜边等于直角边的![]() 倍解答即可.
倍解答即可.
如图,连接PC,
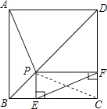
在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
∵PF⊥CD,∠BDC=45°,
∴△PDF是等腰直角三角形,
∴PD=![]() PF,
PF,
又∵矩形的对边PF=EC,
∴PD=![]() EC,故④正确;
EC,故④正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,过点
中点,过点![]() 的直线分别与
的直线分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ;
;
②![]() ;
;
③四边形![]() 是菱形;
是菱形;
④![]() .
.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形△ABC边长为a,等腰三角形△BDC中,∠BDC=120,∠MDN=60,角的两边分别交AB,AC于点M,N,连结MN.则△AMN的周长为( )
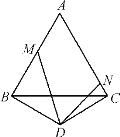
A.aB.2aC.3aD.4a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )

A. 全部正确 B. 仅①和③正确 C. 仅①正确 D. 仅①和②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
爱动脑筋的小明发现二次三项式也可以配方,从而解决一些问题.
例如:x2﹣6x+10=(x2﹣6x+9)+1=(x﹣3)2+1≥0;因此x2﹣6x+10有最小值是1.
(1)尝试:﹣3x2﹣6x+5=﹣3(x2+2x+1﹣1)+5=﹣3(x+1)2+8,因此﹣3x2﹣6x+5有最大值是 .
(2)应用:有长为28米的篱笆,一面利用墙(墙的最大可用长度为16米),围成一个长方形的花圃.能围成面积最大的花圃吗?如果能,请求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:![]() ≈1.41).
≈1.41).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com