
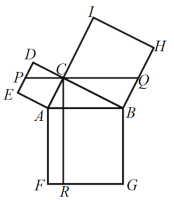
【题目】如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为( )
A.14B.15
C.![]() D.
D.![]()
【答案】A
【解析】
连接EC,CH,设AB交CR于点J,先证得△ECP∽△HCQ,可得![]() ,进而可求得CQ=10,AC:BC=1:2,由此可设AC=a,则BC=2a,利用AC∥BQ,CQ∥AB,可证得四边形ABQC为平行四边形,由此可得AB=CQ=10,再根据勾股定理求得
,进而可求得CQ=10,AC:BC=1:2,由此可设AC=a,则BC=2a,利用AC∥BQ,CQ∥AB,可证得四边形ABQC为平行四边形,由此可得AB=CQ=10,再根据勾股定理求得![]() ,
,![]() ,利用等积法求得
,利用等积法求得![]() ,进而可求得CR的长.
,进而可求得CR的长.
解:如图,连接EC,CH,设AB交CR于点J,
∵四边形ACDE,四边形BCIH都是正方形,
∴∠ACE=∠BCH=45°,
∵∠ACB=90°,∠BCI=90°,
∴∠ACE+∠ACB+∠BCH=180°,∠ACB+∠BCI=180°,
∴点E、C、H在同一直线上,点A、C、I在同一直线上,
∵DE∥AI∥BH,
∴∠CEP=∠CHQ,
∵∠ECP=∠QCH,
∴△ECP∽△HCQ,
∴![]() ,
,
∵PQ=15,
∴PC=5,CQ=10,
∵EC:CH=1:2,
∴AC:BC=1:2,
设AC=a,则BC=2a,
∵PQ⊥CR,CR⊥AB,
∴CQ∥AB,
∵AC∥BQ,CQ∥AB,
∴四边形ABQC为平行四边形,
∴AB=CQ=10,
∵![]() ,
,
∴![]() ,
,
∴![]() (舍负)
(舍负)
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵JR=AF=AB=10,
∴CR=CJ+JR=14,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足AB=CD,AE=DF,CE=BF,连接AF;

(1)连接DE,求证:四边形AEDF是平行四边形;
(2)若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,

活动类型 | 频数(人数) | 频率 |
运动 | 20 | |
娱乐 | 40 | |
阅读 | ||
其他 | 0.1 |
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
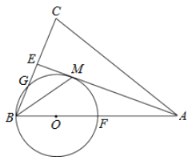
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进单批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.
(1)4月份进了这批T恤衫多少件?
(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
①用含a的代数式表示b;
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
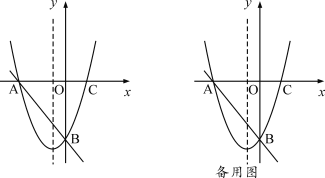
【题目】如图,在平面直角坐标系xoy中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点A和点B.抛物线
轴分别交于点A和点B.抛物线![]() 经过A,B两点,且对称轴为直线
经过A,B两点,且对称轴为直线![]() ,抛物线与
,抛物线与![]() 轴的另一交点为点C.
轴的另一交点为点C.
(1)求抛物线的函数表达式;
(2)设点E是抛物线上一动点,且点E在直线AB下方.当△ABE的面积最大时,求点E的坐标,及△ABE面积的最大值S;
抛物线上是否还存在其它点M,使△ABM的面积等于中的最大值S,若存在,求出满足条件的点M的坐标;若不存在,说明理由;
(3)若点F为线段OB上一动点,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
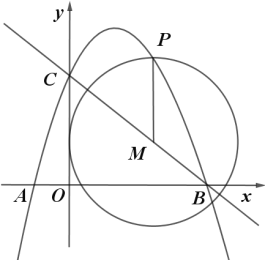
【题目】如图,抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com