
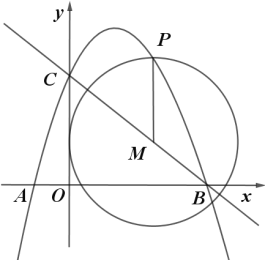
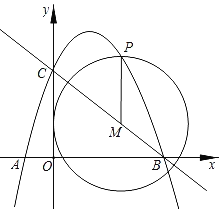
【题目】如图,抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)不存在,理由见解析;(3)⊙M的半径为
x+3;(2)不存在,理由见解析;(3)⊙M的半径为![]() 或
或![]()
【解析】
(1)已知抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N,根据△QCO是等边三角形,求得Q点坐标,再验证Q点是否在抛物线上;
(3)分两种情况①当⊙M与y轴相切,如图所示,令M点横坐标为t,PM=t,将PM用t表示出来,列出关于t的一元二次方程,求得t,进而求得半径;②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示,令M点横坐标为m,因为PN=2MN,列出关于m的一元二次方程,即可求出m,进而求得⊙M的半径.
(1)∵抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3)
x+c经过点A(﹣1,0)和点C(0,3)
∴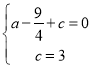
解得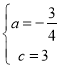
∴该抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+3
x+3
故答案为:y=﹣![]() x2+
x2+![]() x+3
x+3
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N
∵△QCO是等边三角形,OC=3
∴CN=![]()
∴NQ=![]()
即Q(![]() ,
,![]() )
)
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() +3=
+3=![]() ≠
≠![]()
∴Q(![]() ,
,![]() )不在抛物线上
)不在抛物线上
y=﹣![]() x2+
x2+![]() x+3
x+3

故答案为:不存在,理由见解析
(3)①⊙M与y轴相切,如图所示
∵y=﹣![]() x2+
x2+![]() x+3
x+3
当y=0时,﹣![]() x2+
x2+![]() x+3=0
x+3=0
解得x1=-1,x2=4
∴B(4,0)
令直线BC的解析式为y=kx+b
![]()
解得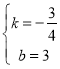
∴直线BC的解析式为![]()
令M点横坐标为t
∵MP∥y轴,⊙M与y轴相切
∴t=﹣![]() t2+
t2+![]() t+3-
t+3-![]()
解得t=![]()
⊙M的半径为![]()
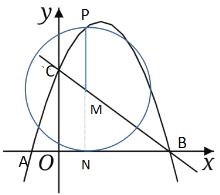
②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示
令M点横坐标为m
∵PN=2MN
∴![]()
解得m=1或m=4(舍去)
∴⊙M的半径为:
![]()
故答案为:⊙M的半径为![]() 或
或![]()


科目:初中数学 来源: 题型:
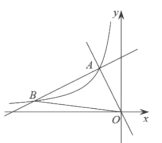
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
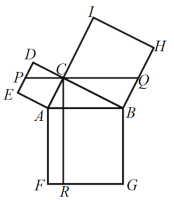
【题目】如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为( )
A.14B.15
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )
A.众数是36.5B.中位数是36.7
C.平均数是36.6D.方差是0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
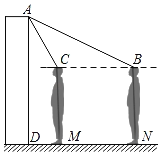
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
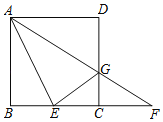
【题目】如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设![]() =λ(λ>0).
=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“停课不停学,学习不延期!”某市教育局为了解初中学生疫情期间在家学习时对一些学习方式的喜好情况,通过微信采用电子问卷的方式随机调查了部分学生(电子调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图,
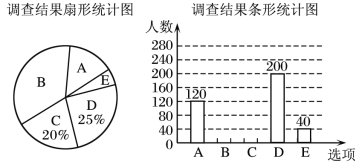
根据以上统计图,解答下列问题:
(1)本次接受调查的学生共有 人;
(2)补全条形统计图;
(3)扇形统计图中,扇形B的圆心角的度数是 度;
(4)若该市约有16万初中生,请估计喜欢自学(选择选项C和D)的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com