
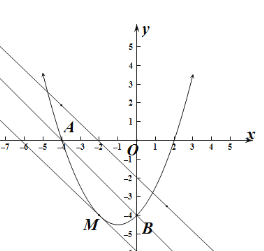
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�A�͵�B.������
��ֱ��ڵ�A�͵�B.������![]() ����A,B���㣬�ҶԳ���Ϊֱ��
����A,B���㣬�ҶԳ���Ϊֱ��![]() ����������
����������![]() �����һ����Ϊ��C.
�����һ����Ϊ��C.
��1���������ߵĺ�������ʽ��
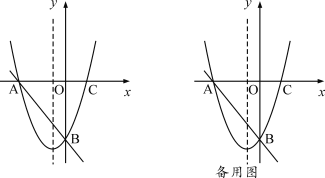
��2�����E����������һ���㣬�ҵ�E��ֱ��AB�·�.����ABE��������ʱ�����E�����꣬����ABE��������ֵS��
���������Ƿ���������M,ʹ��ABM����������е����ֵS,�����ڣ�������������ĵ�M�����ꣻ�������ڣ�˵�����ɣ�
��3������FΪ�߶�OB��һ���㣬ֱ��д��![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() ����2��E(-2,-4��,4�������ڣ�
����2��E(-2,-4��,4�������ڣ�![]() ����3��
����3��![]()
��������
��1�����AB�������꣬���ô���ϵ����������⣻
��2�����E������Ϊ![]() ������ABE��������ʱ����E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b������κ������������飬����ֻ��һ�����㣬��
������ABE��������ʱ����E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b������κ������������飬����ֻ��һ�����㣬��![]() �����b�����������E���ꣻ
�����b�����������E���ꣻ
��������ֱ��AB�Ϸ�������������M,ʹ��ABM����������е����ֵS����ʱ��M����ֱ��![]() ��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ����ֱ��
��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ����ֱ��![]() ����ʽ������κ������������飬������⣻
����ʽ������κ������������飬������⣻
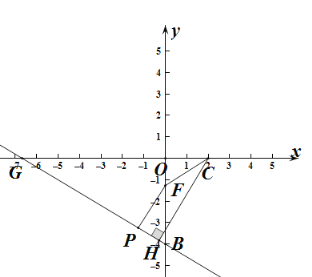
��3����ͼ����![]() ��x���ڵ�G����FP��BG����P���õ�
��x���ڵ�G����FP��BG����P���õ�![]() �����Ե�C��F��P��ͬһֱ����ʱ��
�����Ե�C��F��P��ͬһֱ����ʱ�� ![]() ����Сֵ����CH��GB��H�����CH���ɣ�
����Сֵ����CH��GB��H�����CH���ɣ�
�⣺��1����![]() �зֱ���x=0��y=0���ɵõ�A(-4,0)��B(0,-4)��
�зֱ���x=0��y=0���ɵõ�A(-4,0)��B(0,-4)��
����A,B���꼰�Գ���Ϊֱ��![]() ���ɵ÷�����
���ɵ÷�����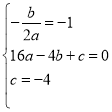
�ⷽ����ɵ�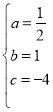
�������ߵĺ�������ʽΪ![]()
��2�������E������Ϊ![]() ������ABE��������ʱ��
������ABE��������ʱ��
��E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b.
�����÷���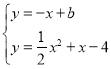 ����ȥy
����ȥy
��![]() ��������
��������![]() ��
��
��֮��![]() ��ֱ��l�Ľ���ʽΪy=-x-6,
��ֱ��l�Ľ���ʽΪy=-x-6,
��������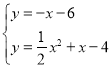 �����
�����![]() ��
��
���E(-2,-4����
��E��y���ƽ���߿������ABE��������ֵΪ4.
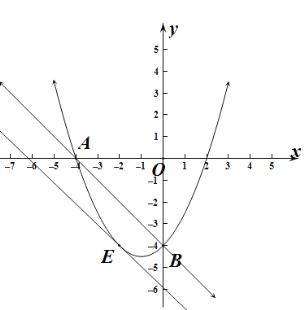
����������ֱ��AB�Ϸ�������������M,ʹ��ABM����������е����ֵS����ʱ��M����ֱ��![]() ��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ���ֱ��
��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ���ֱ��![]() ��ֱ��l����ƽ��4����λ��
��ֱ��l����ƽ��4����λ��
�����ʽ![]() Ϊy=-x-2,����κ�������������ɵ�
Ϊy=-x-2,����κ�������������ɵ�
������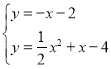 ��֮��
��֮��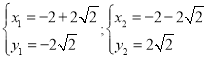
����������㣬![]()
��3����ͼ����![]() ��x���ڵ�G����FP��BG��P��
��x���ڵ�G����FP��BG��P��
��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��![]() ,
,
��![]() ,
,
�൱C��F��P��ͬһֱ����ʱ�� ![]() ����Сֵ��
����Сֵ��
��CH��GB��H��
��![]() ����
���� ![]()
��![]() ,
,![]() ,
,
��A(-4,0)�������߶Գ���Ϊֱ��![]() ��
��
���C������2,0����
��![]() ,
,
�� ��![]() ��
�У�![]() ,
,
��![]() ����СֵΪ
����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�͡�ADE����ͼ��ʾ��ʽ���ã���D�ڡ�ABC�ڣ�����BD��CD��CE���ҡ�DCE��90�㣮

��1����ͼ��������ABC�͡�ADE��Ϊ�ȱ�������ʱ����ȷ��AD��BD��CD�����߶εĹ�ϵ����˵�����ɣ�
��2����ͼ������BA��BC��2AC��DA��DE��2AEʱ����ȷ��AD��BD��CD�����߶εĹ�ϵ����˵�����ɣ�
��3����ͼ������AB��BC��AC��AD��DE��AE��m��n��pʱ����ֱ��д��AD��BD��CD�����߶εĹ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
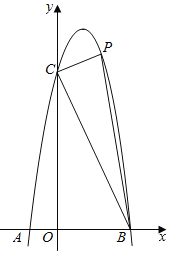
����Ŀ����ͼ����֪������y��ax2+bx+6��������A����1��0����B��3��0����C����������y��Ľ��㣮
��1���������ߵĽ���ʽ��
��2����P��m��n����ƽ��ֱ������ϵ��һ�����ڵ����������˶������PBC�����ΪS����S����m�ĺ�������ʽ��ָ���Ա���m��ȡֵ��Χ����S�����ֵ��
��3����M�����������˶�����N��y�����˶����Ƿ���ڵ�M����Nʹ�á�CMN��90�����ҡ�CMN���OBC���ƣ�������ڣ��������M�͵�N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90������������Ϊ�������������Σ�����C��CR��FG�ڵ�R���ٹ���C��PQ��CR�ֱ�DE��BH�ڵ�P��Q����QH��2PE��PQ��15����CR�ij�Ϊ�� ��
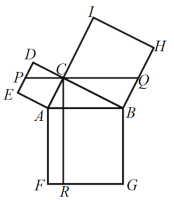
A.14B.15
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ7��ѧ����ij�β������£���λ���棩ʱ�õ��������ݣ�36.3��36.4��36.5��36.7��36.6��36.5��36.5������������������ȷ���ǣ�������
A.������36.5B.�����36.7
C.ƽ������36.6D.������0.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
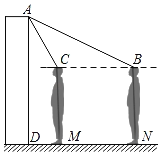
����Ŀ��ijУΪ���ʦ�����£���У�Ű�װ��ij�ͺŲ����ţ���ͼΪ�ò����Ž���ʾ��ͼ����֪������AD�Ķ���A��������Ϊ2.2m��Ϊ�˽��Լ�����Ч�������䣮����1.6m��С����������ʵ�飺�����ڵ���N��ʱ�����ſ�ʼ��ʾ��ͷ�¶ȣ���ʱ�ڶ�ͷB�����A������Ϊ18�����ڵ���M��ʱ��������ֹͣ��ʾ��ͷ�¶ȣ���ʱ�ڶ�ͷC�����A������Ϊ60������С���ڵ������Ч��������MN�ij��ȣ�����ͷ������ľ��������ƣ����㾫ȷ��0.1m��sin18���0.31��cos18���0.95��tan18���0.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��ҵΪ�ӿ��ҵת����������������һ��A��B�����ͺŵĻ�������֪һ̨A�ͻ�����һ̨B�ͻ���ÿСʱ��ӹ�2���������һ̨A�ͻ����ӹ�80�������һ̨B�ͻ����ӹ�60���������ʱ����ȣ�
��1��ÿ̨A��B�����ͺŵĻ���ÿСʱ�ֱ�ӹ����ٸ������
��2���������ҵ�ƻ�����A��B�����ͺŵĻ�����10̨һ��ӹ�һ���������Ϊ�������������Ҫ�����ֻ���ÿСʱ�ӹ������������72����ͬʱΪ�˱��ϻ�����������ת�����ֻ���ÿСʱ�ӹ���������ܳ���76������ôA��B�����ͺŵĻ������Ը����Ŷ���̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
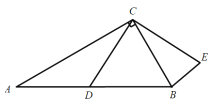
����Ŀ����ͼ����ABC�У���A=30������ACB=90����BC=2��D��AB�ϵĶ��㣬���߶�CD�Ƶ�C��ʱ����ת90�����õ��߶�CE������BE����BE����Сֵ�ǣ� ��
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com