
����Ŀ�������⣺
��1������գ��������������������ɶ������涨����__________��
���ɶ������涨�����������ж�һ����������ֱ�������εķ�������ѧ����һЩ��������ͼ�ε��ж�������ͬ����ͨ���������жϣ�ʵ���ϼ����ڼ�����Ҳ�Ǻ���Ҫ�ģ�����ѧ������������Ͻ�������ѧϰ���ɶ������涨��������Ҫ������չ˼ά����һ�������ѧ�еĸ��ַ�����
��2�����Ķ���С����ѧϰ���ɶ������������ü���ķ���������֤��������������⣺
��ͼ![]() �У�
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ����˵�������߶�
����˵�������߶�![]() ��
��![]() ��
��![]() ���ܹ���һ��ֱ�������Σ�
���ܹ���һ��ֱ�������Σ�
֤������![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��ȥ![]() ����
����![]() ���Ӷ���
���Ӷ���![]() ��
��
����Ϊ��![]() �У�
��![]() ��
��
��ȥ![]() ��
��![]() ����ȥ
����ȥ![]() ������
������![]() ����
����![]() ��
��
���ԣ������߶�![]() ��
��![]() ��
��![]() ���ܹ���һ��ֱ�������Σ�
���ܹ���һ��ֱ�������Σ�
�ɼ��������ڼ���֤����Ҳ�Ǻ���Ҫ�ģ�С���������ô����м��㡢��Ԫ���ֶΣ������ض�������֤�˼������⣮
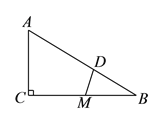
��3����������⣺�ھ���![]() �У���
����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() ��
��![]() ��
��![]() �ϣ�ʹ��
�ϣ�ʹ��![]() ����֤���ı���
����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
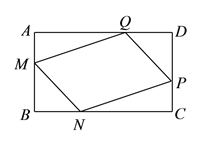
���𰸡�������
�����������������
��1���������������������ɶ������涨�����ɣ�
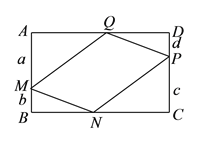
��3����ͼ����AM=a��BM=b��PC=c��PD=d�������֪�ɵã�![]() ��
��![]() ��
��![]() ��
��![]() �����ı���ABCD�Ǿ��οɵ�AB=CD��AD=BC�����г���������a��b��c��d�ĵ�ʽ���ѵ�ʽ���μ���֤��a=c��b=d���Ӷ��ɵ�AM=CP��BM=PD��AQ=CN��DQ=BN����֤��AMQ�ա�CPN����BMN�ա�DPQ������֤��MQ=PN��MN=PQ���Ӷ��ɵ��ı���MNPQ��ƽ���ı���.
�����ı���ABCD�Ǿ��οɵ�AB=CD��AD=BC�����г���������a��b��c��d�ĵ�ʽ���ѵ�ʽ���μ���֤��a=c��b=d���Ӷ��ɵ�AM=CP��BM=PD��AQ=CN��DQ=BN����֤��AMQ�ա�CPN����BMN�ա�DPQ������֤��MQ=PN��MN=PQ���Ӷ��ɵ��ı���MNPQ��ƽ���ı���.
���������
1�����ɶ������涨������Ϊ�����һ�������ε����߳�![]() ��
��![]() ��
��![]() ������
������![]() ��
��
��ô�����������ֱ�������Σ�
3����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�� �ı���![]() Ϊ���Σ�
����
�� ![]() ��
��![]() ��
��
�� 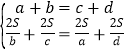 ��
��
�����ã�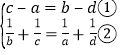 ��
��
�������ã�![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�� ![]() ��
��
�� ![]() ����a=c��
����a=c��
�� b-d=c-a=0��
�� ![]() ��
��
�� AM=CP��BM=PD��AQ=CN��DQ=BN��
���ߡ�A=��B=��C=��D=90�㣬
���AMQ�ա�CPN����BMN�ա�DPQ��
�� ![]() ��
��![]() ��
��
�� �ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�



 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��������������������
��֪����ͼ����AB��CD����B����BFE��180�������B����BFD����D�Ķ�����
�⣺��Ϊ��B����BFE��180����
����AB��EF(����������������)��
����ΪAB��CD��
����CD��EF(����������������)��
���ԡ�CDF����DFE��180��(����������������)��
���ԡ�B����BFD����D����B����BFE����DFE����D��360��.
(2)�������Ͻ�����̽������ͼ����AB��EF����BDF���B����F�к�������ϵ����˵��������
(3)��ͼ�ۢ���AB��EF������̽����ͼ����ͼ������ͼ��������BDF���B����F��������ϵ����ֱ��д�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������в���ʽ��ʽ�����������ǵĽ⼯�������ϱ�ʾ������
(1)5x��15>4x��13����������������������������(2) ![]() ��
��![]() ��
��
(3) ![]() (4)
(4) 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=30����OPƽ����AOB��PD��OB��D��PC��OB��OA��C����PC=6����PD= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̽����
(1)�ֱ�ͼ���С�![]() ���͡�
���͡�![]() ������ֱ��l�ĶԳ�ͼ��(����ʾ��ͼ����)��
������ֱ��l�ĶԳ�ͼ��(����ʾ��ͼ����)��
(2)ͼ����С����С��������ӡ����ĸ�ֱ���ʲô��
(3)����ĸ��![]() ���͡�
���͡�![]() ��д�ڱ�ֽ�����۲�ֽ�ı�����д���㿴������ĸ��Ӱ��
��д�ڱ�ֽ�����۲�ֽ�ı�����д���㿴������ĸ��Ӱ��
(4)С��վ�����ѧ���������������ѧ������ǰ��ij��������ʾ��һ����λ������С��վ�ĵط���(��ͼ����ʾ)�������λ����23456.�����жϳ�����ʾ�����ʵ��λ���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����˶�Աȥ�깲�μ�40������������3�����������Ϊ0.25��ƽ��ÿ����12��3����δͶ�У�
(1)���˶�Աȥ��ı����й�Ͷ�����ٸ�3����Ͷ�ж��ٸ�3����
(2)�����е�һ�������������˶�Ա3������20����С��˵�����˶�Ա�ⳡ������һ��Ͷ����5��3����������ΪС����˵����ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��������Ƶ�ʹ��Ƹ�����������ʱ��ͳ����ijһ������ֵ�Ƶ�ʣ���������ͼ��ʾ������ͳ��ͼ���������һ������������п��ܵ���(����)

A. ����ʯͷ����������������Ϸ����С�������������������
B. һ��ȥ����С������ͨ�˿���ϴ�Ⱥ��������γ�һ���ƵĻ�ɫ�Ǻ���
C. ��������1�������2������������ֻ����ɫ�ϵ�������������ȡһ���ǻ���
D. ��һ���ʵؾ��ȵ������������������ϵ��������4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��P�Ƿ���������y��![]() (k1��0��x��0)ͼ����һ�㣬����P��x�ᡢy��Ĵ��ߣ��ֱ�x�ᡢy����A��B���㣬������������y��
(k1��0��x��0)ͼ����һ�㣬����P��x�ᡢy��Ĵ��ߣ��ֱ�x�ᡢy����A��B���㣬������������y��![]() (0��k2��|k1|)ͼ����E��F���㣮
(0��k2��|k1|)ͼ����E��F���㣮
��1���ú�k1��k2��ʽ�ӱ�ʾ�ı���PEOF�������
��2����P������Ϊ����4��3������PB��PF��2��3���ֱ����k1��k2��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����B��0��1����������OBB1C�����������������ĶԽ���OB1Ϊһ����������OB1B2C1 ����������OB1B2C1�ĶԽ���OB2Ϊһ����������OB2B3C2 ������������OB2B3C2�ĶԽ���OB3Ϊһ����������OB3B4C3 ���������ν�����ȥ�����B6�������ǣ�������

A. ����8��0�� B. ��0����8�� C. ��![]() ��0�� D. ��
��0�� D. ��![]() ��0��
��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com