
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
分析 (1)A家批发需要费用:质量×单价×92%;B家批发需要费用:500×单价×95%+(1000-500)×单价×85%;把相关数值代入求解即可;
(2)根据题意知在A家按零售价的90%优惠价批发的总费用,结合表格将优惠价格分三个层次,逐一表示可得其总费用;
(3)分0~500和500以上~1000两种情况,不超过500千克苹果时,很明显在A家批发更优惠;当他要批发超过500千克但不超过1000千克苹果时,设批发x千克苹果,则A家费用=5.52x,B家费用=5.1x+2850,比较大小即可.
解答 解:(1)A家费用=6×92%×1000=5520,B家费用=6×95%×500+6×85%×500=2850+2550=5400;
故答案为:5200,5400;
(2)A家费用=6×90%x=5.4x,B家费用=6×95%×500+6×85%×1000+6×75%×(x-1500)=4.5x+1200;
故答案为:5.4x,4.5x+1200;
(3)当他要批发不超过500千克苹果时,很明显在A家批发更优惠;
当他要批发超过500千克但不超过1000千克苹果时,
设批发x千克苹果,则A家费用=92%×6x=5.52x,B家费用=6×95%×500+6×85%×(x-500)=5.1x+2850,
A家费用-B家费用=0.42x-2850,
当0.42x=2850,即x=$\frac{5000}{7}$(千克)时,两家的费用相同.
因此,当他要批发$\frac{5000}{7}$千克苹果时,到两家的费用相同;
当他要批发少于$\frac{5000}{7}$千克苹果时,在A家批发更优惠;
当他要批发多于$\frac{5000}{7}$千克苹果时,在B家批发更优惠.
点评 此题考查了列代数式,解题的关键是读懂表格中不同的批发量所对应的优惠幅度,并结合相等关系得出总费用的代数式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一块长30m、宽20m的矩形田地,准备筑同样宽的三条直路,把田地分成六块,种植不同品种的蔬菜,并且种植蔬菜面积为矩形田地面积的$\frac{39}{50}$,则道路的宽为2 m.
如图,有一块长30m、宽20m的矩形田地,准备筑同样宽的三条直路,把田地分成六块,种植不同品种的蔬菜,并且种植蔬菜面积为矩形田地面积的$\frac{39}{50}$,则道路的宽为2 m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
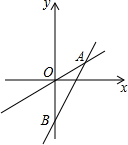 如图表示一个正比例函数y1=k1x与一个一次函数y2=k2x+b的图象,它们交于点
如图表示一个正比例函数y1=k1x与一个一次函数y2=k2x+b的图象,它们交于点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com