
分析 (1)根据函数的增减性得到m-3>0,从而确定m的取值范围;
(2)根据正比例函数的定义得到m-3≠0且m-8=0,从而确定m的值;
(3)根据一次函数的性质确定m的取值范围,然后从m的范围内确定m的一个值即可.
解答 解:(1)根据题意得m-3>0,
解得m>3;
(2)根号题意得m-3≠0且m-8=0,
解得m=8;
(3)根据题意得:
$\left\{\begin{array}{l}{m-3>0}\\{m-8<0}\end{array}\right.$,
解得:3<m<8,
∴3<m<8中任取一个值都可以.
点评 本题考查了一次函数图象与系数的关系及正比例函数的定义,解题的关键是了解一次函数的性质,难度不大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
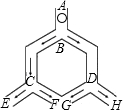 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+x)2=73 | B. | 1+x+x2=73 | C. | (1+x)x=73 | D. | 1+x+2x=73 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
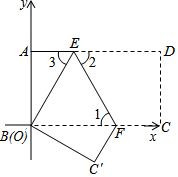 如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com