
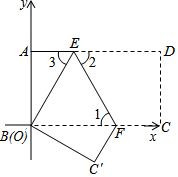
 如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.分析 (1)可以假设∠1=3x,∠3=4x,由∠3+∠FEB+∠2=180°,∠2=∠FEB=3x,列出方程即可解决问题.
(2)①设AE=a,则EB=ED=6.4-x,在Rt△AEB中,由AB2+AE2=EO2,可得4.82+x2=(6.4-x)2,解方程即可.
②作EH⊥OC于H,则四边形AOHE是矩形,EH=OA=4.8,先求出EO、OF,分两种情形①当点P在OE上时,作P1M⊥EF于M,P1N⊥OF于N,
根据$\frac{{S}_{△EF{P}_{1}}}{{S}_{△OF{P}_{1}}}$=$\frac{\frac{1}{2}•EF•{P}_{1}M}{\frac{1}{2}•OF•{P}_{1}N}$=$\frac{{P}_{1}E}{{P}_{1}O}$=$\frac{6}{5}$,由此即可求出OP.②当点P在EF上时,由OE=OF,可知EP2=FP2时,点P到OE,OF两边距离相等,由此即可解决问题.
解答 解:(1)∵∠1:∠3=3:4,
∴可以假设∠1=3x,∠3=4x,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAB=90°,
∴∠2=∠1=3x,
∵∠3+∠FEB+∠2=180°,∠2=∠FEB=3x,
∴4x+3x+3x=180°,
∴x=18°,
∴∠3=4x=72°.
(2)①设AE=a,则EB=ED=6.4-x,
在Rt△AEB中,∵AB2+AE2=EO2,
∴4.82+x2=(6.4-x)2,
∴x=1.4,
∴点E坐标(1.4,4.8).
②作EH⊥OC于H,则四边形AOHE是矩形,EH=OA=4.8,
由①可知,EO=$\sqrt{A{E}^{2}+O{A}^{2}}$=$\sqrt{4.{8}^{2}{+1.4}^{2}}$=5,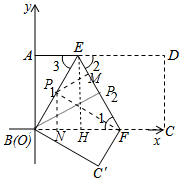
∵∠OEF=∠1,
∴OE=OF=5,
∴EF=$\sqrt{E{H}^{2}+H{F}^{2}}$=$\sqrt{4.{8}^{2}+3.{6}^{2}}$=6.
a、当点P在OE上时,作P1M⊥EF于M,P1N⊥OF于N,
如果P1M=P1N,
则有$\frac{{S}_{△EF{P}_{1}}}{{S}_{△OF{P}_{1}}}$=$\frac{\frac{1}{2}•EF•{P}_{1}M}{\frac{1}{2}•OF•{P}_{1}N}$=$\frac{{P}_{1}E}{{P}_{1}O}$=$\frac{6}{5}$,
∴OP1=$\frac{5}{11}$×5=$\frac{25}{11}$,
∴t=$\frac{25}{11}$s时.
b、当点P在EF上时,∵OE=OF,
∴EP2=FP2时,点P到OE,OF两边距离相等,
此时t=5+3=8s.
综上所述,t=$\frac{25}{11}$s或8s时,点P到△BEF的两边的距离相等.
点评 本题考查四边形综合题、坐标与图形的性质、勾股定理、角平分线的性质定理等知识,解题的关键是熟练应用所学知识,学会利用面积法求有关线段,属于中考压轴题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,21007) | B. | ( 21007,-21007) | C. | ( 21008,-21008) | D. | ( 0,21008) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com