
分析 首先把A(0,-2)、B(3,1)代入y=kx+b,可得关于k、b的方程组,解方程组可得k、b的值,进而可得一次函数解析式,然后再把C点坐标代入函数解析式可得M的值.
解答 解:∵一次函数y=kx+b的图象经过点A(0,-2)、B(3,1),
∴$\left\{\begin{array}{l}{-2=b}\\{1=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴一次函数解析式为y=x-2,
∵图象过C(m,-4),
∴-4=m-2,
解得:m=-2.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点,必能满足解析式.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,21007) | B. | ( 21007,-21007) | C. | ( 21008,-21008) | D. | ( 0,21008) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
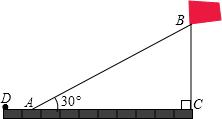 如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com