

分析 图形理解:根据已知可得两张粘合重合一次,粘合n张,重合n-1部分,从而得出结论;
问题解决:结合长方形面积公式,可列出关于n的一元一次方程,解出方程即是所求;
拓展应用:设分给霞霞x张,则分给瑶瑶30-x张.结合题意列出关于x的一元一次方程,解出方程即是所求.
解答 解:图形理解:
粘合2张白纸条,则DC=30×2-a=60-acm,D1C1=10×2-b=20-bcm;
粘合n张白纸条,则DC=30n-a(n-1)cm,D1C1=10n-b(n-1)cm.
故答案为:60-a;20-b;30n-a(n-1);10n-b(n-1).
问题解决:
由题意可得:10×[30×7-6×(7-1)]=30×[10n-6×(n-1)],
∴1560=120n,∴n=13.
答:n的值为13.
拓展应用:
设分给霞霞x张,则分给瑶瑶30-x张.
根据题意得:10×[30x-6(x-1)]=30×[10×(30-x)-4×(30-x-1)],
即420x=5460,解得x=13,则30-x=17.
答:应分配给霞霞13张,瑶瑶17张.
点评 本题考查了一元一次方程的应用,解题的关键:弄明白粘合n张,重合了n-1个部分,再结合面积公式列出方程.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 抛出一枚硬币,落地后正面向上 | |
| B. | 打开电视,正在播放广告 | |
| C. | 篮球队员在罚球线投篮一次,未投中 | |
| D. | 实心铁球投入水中会沉入水底 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,请按照要求回答问题.
如图,请按照要求回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
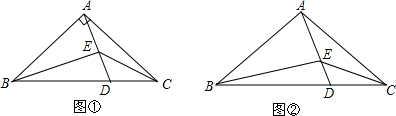
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com