【题目】长方形
中，
边的长为
,
边的长为
,
是长方形边上的一个动点，当
三点构成的三角形为等腰三角形时，
的长为________.
【答案】
或
或
【解析】
当
三点构成的三角形为等腰三角形时，分三种情况：①当AE=AD时，②当DE=AD，③当AE=DE时，根据等腰三角形的性质分别求解即可.
∵在长方形
中，
边的长为
，
边的长为
，
∴AB=DC=，AD=BC=，∠BAD=∠ABC=∠BCD=∠ADC=90°，
∵
是长方形边上的一个动点，当三点构成的三角形为等腰三角形时，
①当AE=AD时，如图：
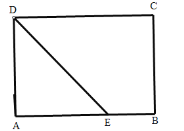
∵AE=AD=6cm，
∴BE=AB-AE=8-6=2cm；
②当DE=AD，如图：
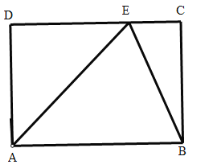
∵DE=AD=6cm，
∴CE=DC-DE=2，
∴在直角△BCE中，
（cm）；
③当AE=DE时，如图：
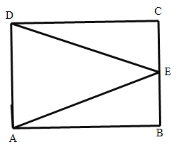
∵点E在线段AD的垂直平分线上，
∴点E是BC的中点，
∴
，
综上所述，BE的长为
或
或
；
故答案为：或或.
浙江名校名师金卷系列答案
全优冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
（1）求证：四边形ADCF是菱形；
（3）若AC＝6，AB＝8，求菱形ADCF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（感知）如图①，点C是AB中点，CD⊥AB，P是CD上任意一点，由三角形全等的判定方法“SAS”易证△PAC≌△PBC，得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”
（探究）如图②，在平面直角坐标系中，直线y=-
x+1分别交x轴、y轴于点A和点B，点C是AB中点，CD⊥AB交OA于点D，连结BD，求BD的长
（应用）如图③
（1）将线段AB绕点A顺时针旋转90°得到线段AB′，请在图③网格中画出线段AB;
（2）若存在一点P，使得PA=PB′，且∠APB′≠90°，当点P的横、纵坐标均为整数时，则AP长度的最小值为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁，
（I）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至A'C'的位置时，A'C'的长为 .
（II）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
＝
与
轴交于
，
两点，与轴交于点
．
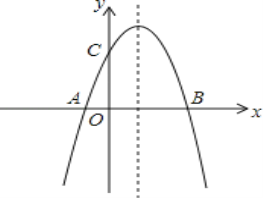
（1）求抛物线的解析式及顶点
坐标；
（2）在抛物线的对称轴上找到点
，使得
的周长最小，并求出点的坐标；
（3）在（2）的条件下，若点
是线段
上的一个动点（不与点
、
重合）．过点作
交轴于点
．设
的长为
，问当取何值时，
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展，小明计划给朋友快递一部分物品，经了解有甲乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．
（1）根据题意，填写下表：
重量（千克） 费用（元） | 0.5 | 1 | 3 | 4 | … |
甲公司 | _________ | 22 | _________ | 67 | … |
乙公司 | 11 | ________ | 51 | _________ | … |
（2）请分别写出甲乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（3）小明应选择哪家快递公司更省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究．
（一）猜测探究
在△ABC中，AB＝AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度，得到线段AN，连接NB．
（1)如图1，若M是线段BC上的任意一点，请直接写出∠NAB与∠MAC的数量关系是_______，NB与MC的数量关系是_______；
（2)如图2，点E是AB延长线上点，若M是∠CBE内部射线BD上任意一点，连接MC，（1)中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由。
（二)拓展应用
如图3，在△A1B1C1中，A1B1＝8，∠A1B1C1＝90°，∠C1＝30°，P是B1C1上的任意点，连接A1P，将A1P绕点A1按顺时针方向旅转60°，得到线段A1Q，连接B1Q．求线段B1Q长度的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
：
是由抛物线
：
平移得到的，并且的顶点为（1，－4）
（1）求
的值；
（2）如图1，抛物线C1与x轴正半轴交于点A，直线
经过点A，交抛物线C1于另一点B．请你在线段AB上取点P，过点P作直线PQ∥y轴交抛物线C1于点Q，连接AQ．
①若AP＝AQ，求点P的坐标；
②若PA＝PQ，求点P的横坐标．
（3）如图2，△MNE的顶点M、N在抛物线C2上，点M在点N右边，两条直线ME、NE与抛物线C2均有唯一公共点，ME、NE均与y轴不平行．若△MNE的面积为16，设M、N两点的横坐标分别为m、n，求m与n的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
