
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
甲公司 | _________ | 22 | _________ | 67 | … |
乙公司 | 11 | ________ | 51 | _________ | … |
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
【答案】(1)11;52;19;67;(2)y甲![]() ;y乙=16x+3(x>0);(3)当快递物品少于
;y乙=16x+3(x>0);(3)当快递物品少于![]() 千克或多于4千克时,选择甲公司省钱;当快递物品等于
千克或多于4千克时,选择甲公司省钱;当快递物品等于![]() 千克或等于4千克时,两家公司费用一样;当快递物品多于
千克或等于4千克时,两家公司费用一样;当快递物品多于![]() 千克而少于4千克时,选择乙公司省钱.
千克而少于4千克时,选择乙公司省钱.
【解析】
(1)根据甲、乙公司的收费方式,求出y值即可;
(2)根据甲、乙公司的收费方式结合数量关系,找出y甲、y乙(元)与x(千克)之间的函数关系式;
(3)分0<x≤1和x>1两种情况,分别求出y甲>y乙、y甲=y乙、y甲<y乙时x的取值范围,综上即可得出结论.
解:(1)当x=0.5时,y甲=22×0.5=11;
当x=3时,y甲=22+15×2=52;
当x=1时,y乙=16×1+3=19;
当x=4时,y乙=16×4+3=67.
故答案为:11;52;19;67.
(2)当0<x≤1时,y甲=22x;
当x>1时,y甲=22+15(x﹣1)=15x+7.
∴y甲![]() .
.
y乙=16x+3(x>0).
(3)若0<x≤1,当y甲>y乙时,有22x>16x+3,
解得:![]() ;
;
当y甲=y乙时,有22x=16x+3,
解得:![]() ;
;
当y甲<y乙时,有22x<16x+3,
解得:![]() ;
;
若x>1,当y甲>y乙时,有15x+7>16x+3,
解得:x<4;
当y甲=y乙时,有15x+7=16x+3,
解得:x=4;
当y甲<y乙时,有15x+7<16x+3,
解得:x>4.
综上可知:当快递物品少于![]() 千克或多于4千克时,选择甲公司省钱;当快递物品等于
千克或多于4千克时,选择甲公司省钱;当快递物品等于![]() 千克或等于4千克时,两家公司费用一样;当快递物品多于
千克或等于4千克时,两家公司费用一样;当快递物品多于![]() 千克而少于4千克时,选择乙公司省钱.
千克而少于4千克时,选择乙公司省钱.
故答案为(1)11;52;19;67;(2)y甲![]() ;y乙=16x+3(x>0);(3)当快递物品少于
;y乙=16x+3(x>0);(3)当快递物品少于![]() 千克或多于4千克时,选择甲公司省钱;当快递物品等于
千克或多于4千克时,选择甲公司省钱;当快递物品等于![]() 千克或等于4千克时,两家公司费用一样;当快递物品多于
千克或等于4千克时,两家公司费用一样;当快递物品多于![]() 千克而少于4千克时,选择乙公司省钱.
千克而少于4千克时,选择乙公司省钱.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
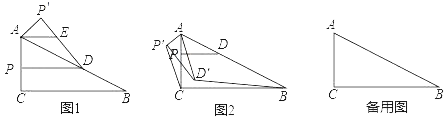
【题目】Rt△ABC中,∠ACB=90°,AC=3,BC=7,点P是边AC上不与点A、C重合的一点,作PD∥BC交AB边于点D.
(1)如图1,将△APD沿直线AB翻折,得到△AP'D,作AE∥PD.求证:AE=ED;
(2)将△APD绕点A顺时针旋转,得到△AP'D',点P、D的对应点分别为点P'、D',
①如图2,当点D'在△ABC内部时,连接P′C和D'B,求证:△AP'C∽△AD'B;
②如果AP:PC=5:1,连接DD',且DD'=![]() AD,那么请直接写出点D'到直线BC的距离.
AD,那么请直接写出点D'到直线BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
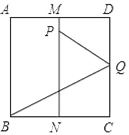
【题目】如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
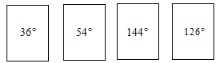
【题目】如图,有四张质地完全相同的卡片,正面分别写有四个角度,现将这四张卡片洗匀后,背面朝上.
(1)若从中任意抽取--张,求抽到锐角卡片的概宰;
(2)若从中任意抽取两张,求抽到的两张角度恰好互补的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
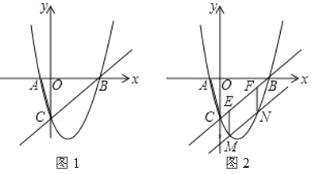
【题目】如图1,二次函数y=ax2﹣3ax﹣4a的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣3).
(1)求二次函数的表达式及点A、点B的坐标;
(2)若点D在二次函数图象上,且![]() ,求点D的横坐标;
,求点D的横坐标;
(3)将直线BC向下平移,与二次函数图象交于M,N两点(M在N左侧),如图2,过M作ME∥y轴,与直线BC交于点E,过N作NF∥y轴,与直线BC交于点F,当MN+ME的值最大时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:①当CD⊥AB时,EF为△ABC的中位线;②当四边形CEDF为矩形时,AC=BC;③当点D为AB的中点时,△CEF与△ABC相似;④当△CEF与△ABC相似时,点D为AB的中点.其中正确的是_____(把所有正确的结论的序号都填在横线上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com