
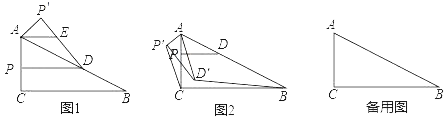
【题目】Rt△ABC中,∠ACB=90°,AC=3,BC=7,点P是边AC上不与点A、C重合的一点,作PD∥BC交AB边于点D.
(1)如图1,将△APD沿直线AB翻折,得到△AP'D,作AE∥PD.求证:AE=ED;
(2)将△APD绕点A顺时针旋转,得到△AP'D',点P、D的对应点分别为点P'、D',
①如图2,当点D'在△ABC内部时,连接P′C和D'B,求证:△AP'C∽△AD'B;
②如果AP:PC=5:1,连接DD',且DD'=![]() AD,那么请直接写出点D'到直线BC的距离.
AD,那么请直接写出点D'到直线BC的距离.
【答案】(1)见解析;(2)①见解析;②点D'到直线BC的距离为![]() 或
或![]()
【解析】
(1)由折叠的性质和平行线的性质可得∠EAD=∠ADP=∠ADP',即可得AE=DE;
(2)①由题意可证△APD∽△ACB,可得![]() ,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,,则△AP'C∽△AD'B;②分点D'在直线BC的下方和点D'在直线BC的上方
,由旋转的性质可得AP=AP',AD=AD',∠PAD=∠P'AD',即∠P'AC=∠D'AB,,则△AP'C∽△AD'B;②分点D'在直线BC的下方和点D'在直线BC的上方![]() 两种情况讨论,根据平行线分线段成比例,可求PD=
两种情况讨论,根据平行线分线段成比例,可求PD=![]() ,通过证明△AMD'≌△DPA,可得AM=PD=
,通过证明△AMD'≌△DPA,可得AM=PD=![]() ,即可求点D'到直线BC的距离.
,即可求点D'到直线BC的距离.
证明:(1)∵将△APD沿直线AB翻折,得到△AP'D,
∴∠ADP'=∠ADP,
∵AE∥PD,
∴∠EAD=∠ADP,
∴∠EAD=∠ADP',
∴AE=DE
(2)①∵DP∥BC,
∴△APD∽△ACB,
∴![]() ,
,
∵旋转,
∴AP=AP',AD=AD',∠PAD=∠P'AD',
∴∠P'AC=∠D'AB,![]() ,
,
∴△AP'C∽△AD'B
②若点D'在直线BC下方,如图,过点A作AF⊥DD',过点D'作D'M⊥AC,交AC的延长线于M,
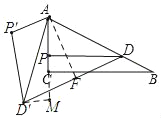
∵AP:PC=5:1,
∴AP:AC=5:6,
∵PD∥BC,
∴![]() =
=![]() ,
,
∵BC=7,
∴PD=![]() ,
,
∵旋转,
∴AD=AD',且AF⊥DD',
∴DF=D'F=![]() D'D,∠ADF=∠AD'F,
D'D,∠ADF=∠AD'F,
∵cos∠ADF=![]() =
=![]() =
=![]()
![]() ,
,
∴∠ADF=45°,
∴∠AD'F=45°,
∴∠D'AD=90°
∴∠D'AM+∠PAD=90°,
∵D'M⊥AM,
∴∠D'AM+∠AD'M=90°,
∴∠PAD=∠AD'M,且AD'=AD,∠AMD'=∠APD,
∴△AD'M≌△DAP(AAS)
∴PD=AM=![]() ,
,
∵CM=AM﹣AC=![]() ﹣3,
﹣3,
∴CM=![]() ,
,
∴点D'到直线BC的距离为![]()
若点D'在直线BC的上方,如图,过点D'作D'M⊥AC,交CA的延长线于点M,
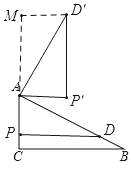
同理可证:△AMD'≌△DPA,
∴AM=PD=![]() ,
,
∵CM=AC+AM,
∴CM=3+![]() =
=![]() ,
,
∴点D'到直线BC的距离为![]()
综上所述:点D'到直线BC的距离为![]() 或
或![]() ;
;


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
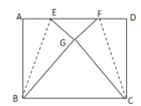
【题目】如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=![]() ,BC=2,求EF的长.
,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点E在CD上,∠AEB=90°,点P从点A出发,沿A→E→B的路径匀速运动到点B停止,作PQ⊥CD于点Q,设点P运动的路程为x,PQ长为y,若y与x之间的函数关系图象如图2所示,当x=6时,PQ的值是( )
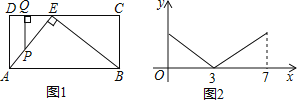
A. 2B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() ,点
,点![]() ,点
,点![]() ,动点
,动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 、
、![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() 、
、![]() .
.
(1)若点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
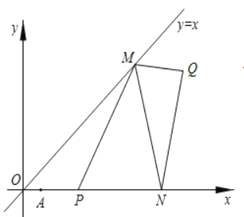
(2)如图![]() ,当
,当![]() 周长最小时,连接
周长最小时,连接![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
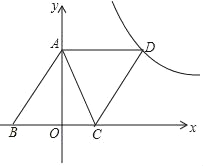
【题目】如图,直线y=﹣2x+4与x轴,y轴分别交于点C,A,点D为点B(﹣3,0)关于AC的对称点,反比例函数y=![]() 的图象经过点D.
的图象经过点D.
(1)求证:四边形ABCD为菱形;
(2)求反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
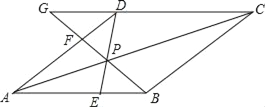
【题目】如图,点P是ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交AD于点F,交CD的延长线于点G,已知![]() .
.
(1)求![]() 的值.
的值.
(2)若四边形ABCD是菱形.
①求证:△APB≌△APD;
②若DP的长为6,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
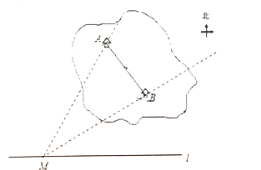
【题目】小强想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道I上某一观测点M处,测得亭A在点M的北偏东30°,亭B在点M的北偏东60°,当小明由点M沿小道I向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小强计算湖中两个小亭A、B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com