练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，7个腰长为1的等腰直角三角形(Rt△B1AA1，Rt△B2A1A2，Rt△B3A2A3…)有一条腰在同一条直线上，设△A1B2C1的面积为S1，△A2B3C2的面积为S2，△A3B4C3的面积为S3，则阴影部分的面积是______ .

    【答案】

    【解析】

    连接B1、B2、B3、B4点，显然它们共线且平行于AC1，依题意可知△B1B2C1与△C1AA1相似，求出相似比，根据三角形面积公式可得出S1，同理：B2B3：AA2=1：2，所以B2C2：C2A=1：2，进而求出S2、 S3…S7，最后求和即可.

    解：连接B1、B2、B3、Ba.

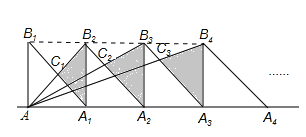
    ∵7个边长为1的等腰三角形有一条边在同一直线上，

    ∴ 连接B1、B2、B3点，显然它们共线且平行于AA1

    ∴S1=

    ∵B2B3∥AA2，

    ∴△B2C2B3∽△A2C2A，

    ∴

    ∴S2=SA2B3B2=×=

    同理：S3= ×=，S4= ×=，S5= ×=，S6= ×=，S7= ×=，

    ∴阴影部分的面积为：++++++=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某面粉厂生产某品牌的面粉按质量分5个档次，生产第一档（最低档次）面粉，每天能生产55吨，每吨利润1000元.生产面粉的质量每提高一个档次，每吨利润会增加200元，但每天的产量会减少5吨.

    （1）若生产第档次的面粉每天的总利润为元（其中为正整数，且），求生产哪个档次的面粉时，每天的利润最大，每天的最大利润是多少元？

    （2）若生产第档次的面粉一天的总利润为60000元，求该面粉的质量档次.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y＝﹣x2+bx+c与x轴交于原点O和点A（6，0），抛物线的顶点为B．

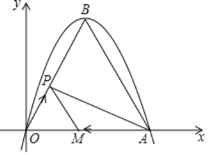
    （1）求该抛物线的解析式和顶点B的坐标；

    （2）若动点P从原点O出发，以每秒1个长度单位的速度沿线段OB运动，设点P运动的时间为t（s）．问当t为何值时，△OPA是直角三角形？

    （3）若同时有一动点M从点A出发，以2个长度单位的速度沿线段AO运动，当P、M其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t（s），连接MP，当t为何值时，四边形ABPM的面积最小？并求此最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点C是的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．

    （1）求证：BD是⊙O的切线；（2）当OB＝2时，求BH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

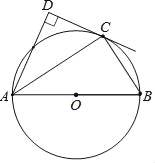
    【题目】如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D．

    （1）求证：AC平分∠DAB；

    （2）求证：AC2=ADAB；

    （3）若AD=，sinB=，求线段BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝2x+6与反比例函数的图象交于点A（1，m），与x轴交于点B，平行于x轴的直线y＝n（0＜n＜6）交反比例函数的图象于点M，交AB于点N，连接BM．

    （1）求m的值和反比例函数的表达式；

    （2）观察图象，直接写出当x＞0时，不等式2x+6-＜0的解集；

    （3）当n为何值时，△BMN的面积最大？最大值是多少？

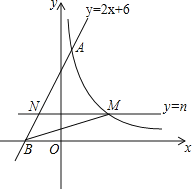
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，，P是BC上一动点，过P作AP的垂线交CD于E，将翻折得到，延长FP交AB于H，连结AE，PE交AC于G.

    （1）求证；

    （2）当时，求AE的长；

    （3）当时，求AG的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

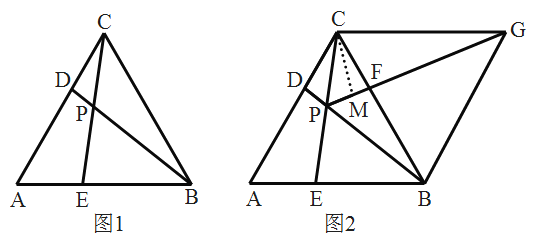
    【题目】如图，是等边三角形，点，分别在上，且，与相交于点.

    （1）求证：；

    （2）如图2，将沿直线翻折得到对应的，过点作，交射线于点，与相交于点，连接.

    ①试判断四边形的形状，并说明理由.

    ②若四边形的面积为，，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

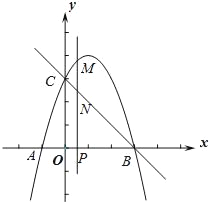
    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（﹣1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．

    （1）求抛物线的解析式和直线BC的解析式；

    （2）当点P在线段OB上运动时，若△CMN是以MN为腰的等腰直角三角形时，求m的值；

    （3）当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时，求m的值．

    查看答案和解析>>

    同步练习册答案