
【题目】如图,已知二次函数![]() (a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0,②4a+2b+c>0,③![]() <8a,④
<8a,④![]() <a<
<a<![]() ,⑤b>c.
,⑤b>c.
其中含所有正确结论的选项是( )
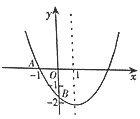
A.①③ B.①③④ C.②④⑤ D.①③④⑤
【答案】D.
【解析】
试题分析:①∵函数开口方向向上,∴a>0;∵对称轴在原点左侧,∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;
②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=﹣1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;
③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1,∴![]() =1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴
=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴![]() =4a(﹣3a)﹣
=4a(﹣3a)﹣![]() =
=![]() <0,∵8a>0,∴
<0,∵8a>0,∴![]() <8a,故③正确;
<8a,故③正确;
④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1,∴﹣2<﹣3a<﹣1,∴![]() >a>
>a>![]() ;故④正确;
;故④正确;
⑤∵a>0,∴b﹣c>0,即b>c;故⑤正确;
故选D.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2
B.a>2
C.a<﹣2
D.a<2且a≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
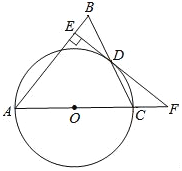
【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若EB=![]() ,且sin∠CFD=
,且sin∠CFD=![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式的值
(1)已知x= ![]() ,y=
,y= ![]() ,求代数式(2x+3y)2﹣(2x﹣3y)2的值.
,求代数式(2x+3y)2﹣(2x﹣3y)2的值.
(2)已知a﹣b=5,ab=1,求a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )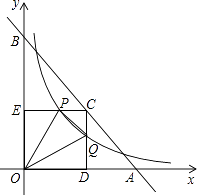
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
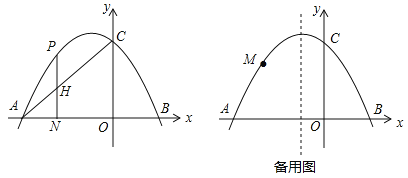
【题目】如图,在平面直角坐标系中,抛物线![]() 交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=
交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com