Question

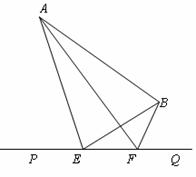
如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，

∠BFQ＝60°，EF＝1km．

⑴判断线段AB与AE的数量关系，并说明理由；

⑵求两个岛屿A和B之间的距离（结果精确到0.1km）．

 

Answer 1

 （1）相等．   （1分）     
理由如下：∵∠BEQ=30°，∠BFQ=60°，

∴∠EBF=30°，EF=BF．                         
又∵∠AFP=60°，∴∠BFA=60°．（2分）    
在△AEF与△ABF中，
EF=BF，∠AFE=∠AFB，AF=AF，
∴△AEF≌△ABF，（3分）    
∴AB=AE．            （4分）     

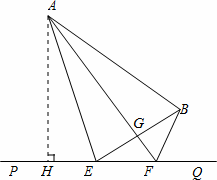（2）方法一：作AH⊥PQ，垂足为H．
设AE=x，
则AH=xsin74°，HE=xcos74°，（5分）
HF=xcos74°+1．                             （6分）   
Rt△AHF中，AH=HF•tan60°，
∴xsin74°=（xcos74°+1）•tan60°，（7分）
即0.96x=（0.28x+1）×1.73，
解得x≈3.6，即AB≈3.6．
答：两个岛屿A与B之间的距离约为3.6km．          （8分）
方法二：设AF与BE的交点为G．
在Rt△EGF中，∵EF=1，∴EG=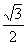．          （6分）   
在Rt△AEG中，
∠AEG=76°，AE=EG÷cos76°=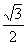÷0.24≈3.6km，（7分）
∵AE=AB，  

∴两个岛屿A和B之间的距离是3.6km，（8分）