
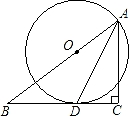
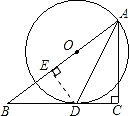
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
【考点】切线的判定.
【专题】几何综合题.
【分析】(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
【解答】(1)证明:连接OD;
∵AD是∠BAC的平分线,
∴∠1=∠3.(1分)
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴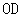 ∥AC.(2分)
∥AC.(2分)
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.(3分)
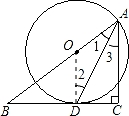
(2)解:过点D作DE⊥AB,
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得: ,(4分)
,(4分)
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.(5分)
∴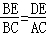 .
.
∴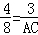 .
.
∴AC=6.(6分)
【点评】本题综合性较强,既考查了切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了角平分线的性质,勾股定理得到BE的长,及相似三角形的性质.


科目:初中数学 来源: 题型:
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )

A. B.
B. C.
C. D.π
D.π
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人中恰好1人选修篮球,1人选修足球的概率.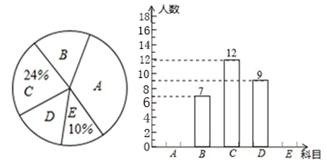
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离 cm.
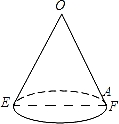
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com